¶ 2024 AIME I Problem 11
Problem:
Each vertex of a regular octagon is independently colored either red or blue with equal probability. The probability that the octagon can then be rotated so that all of the blue vertices move to positions where there had been red vertices is , where and are relatively prime positive integers. Find .
Solution:
There are equally likely ways to color the vertices of the octagon. If more than of the vertices are colored blue, then it is not possible to rotate the octagon so that blue vertices move to positions previously occupied by red vertices. If or fewer of the vertices are colored blue, then it is always possible to rotate the octagon so that the blue vertices move to positions where there had been red vertices. Indeed, if there are at most blue vertices, then there are at most rotations that move a particular blue vertex onto a position of a different blue vertex. Thus there are at most rotations that move at least one blue vertex onto the position of another blue vertex. Because there are possible rotations that move the vertices, there must be at least one rotation that moves all blue vertices to positions where there were red vertices. The number of ways to color or fewer vertices blue is .
It is left to count the number of ways to color of the vertices blue and have an acceptable rotation. Each coloring with blue vertices is a rotation or reflection and rotation of one of the following eight patterns: the first with no two blue vertices adjacent, the second with blue vertices adjacent, the third and fourth with blue vertices adjacent, and the last four with blue vertices adjacent.
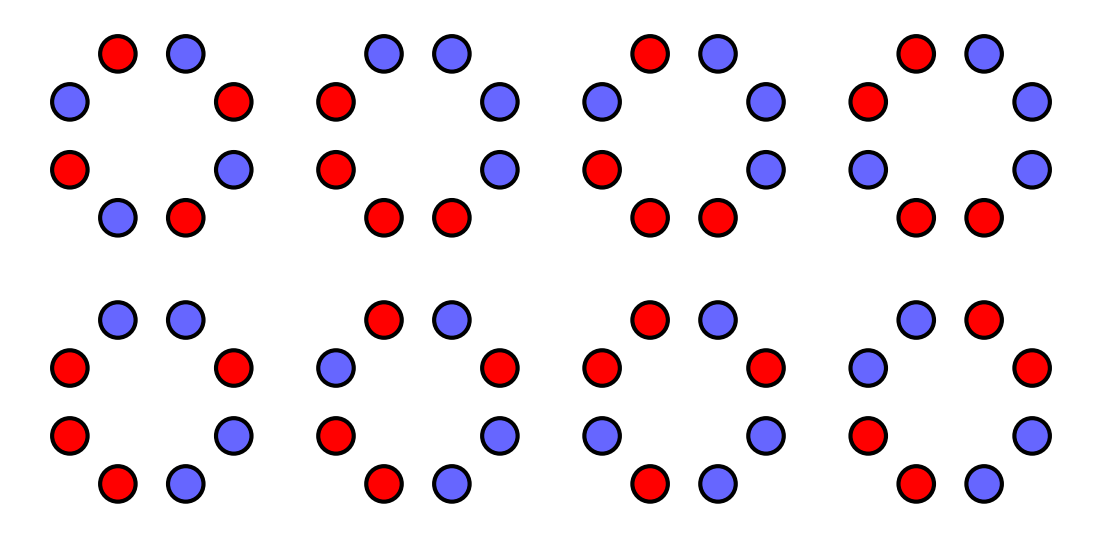
The first, second, seventh, and eighth of these colorings have acceptable rotations while the other four colorings do not have acceptable rotations. There are and colorings of the vertices similar to the first, second, seventh, and eighth colorings, respectively, giving colorings with blue vertices that have acceptable rotations.
The total number of colorings with acceptable rotations is . The required probability is . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions