¶ 2024 AIME I Problem 12
Problem:
Define and . Find the number of intersections of the graphs of
Solution:
The graph of on the interval traces one complete period of the sine wave, where oscillates from to to and back to . Thus the graph of oscillates . It then follows that the graph of oscillates , as shown.
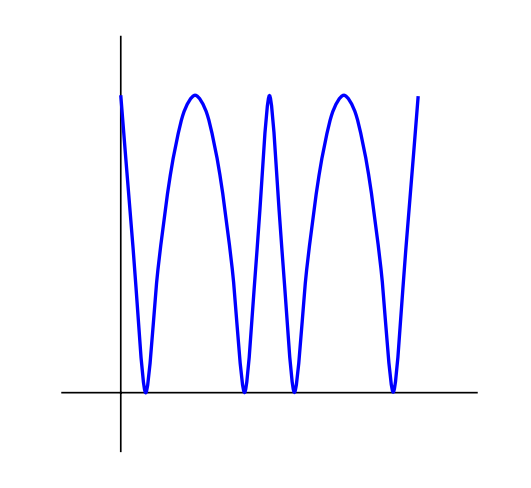
Note that this graph passes through and , and it zigzags down and up between the lines and a total of times in this interval. In particular, there are intersection points between this graph and the line . Therefore the curve goes through and , and consists of monotonically decreasing sections which alternate with monotonically increasing sections, where each section has endpoints on the lines and . Similarly, the curve goes through and and consists of monotonically decreasing sections which alternate with monotonically increasing sections, where each section has endpoints on the lines and . These curves have no intersections outside the unit square with vertices at and .
The only intersection of the two curves on the boundary of the unit square is at the point . Because the graph of crosses the line without being tangent to it, the curve meets the line at without being tangent to it. However, because the graph of is tangent to the -axis at , the curve is tangent to the line at . As a result, the rightmost monotonically increasing section of the curve intersects the uppermost monotonically increasing section of the curve at a point in the interior of the square. Therefore the number of intersections between these curves in the interior of the square is the same as the number of intersections between a set of vertical lines and horizontal lines, which is . Because the curves also intersect at on the boundary of the square, the two curves intersect at a total of points.
The problems on this page are the property of the MAA's American Mathematics Competitions