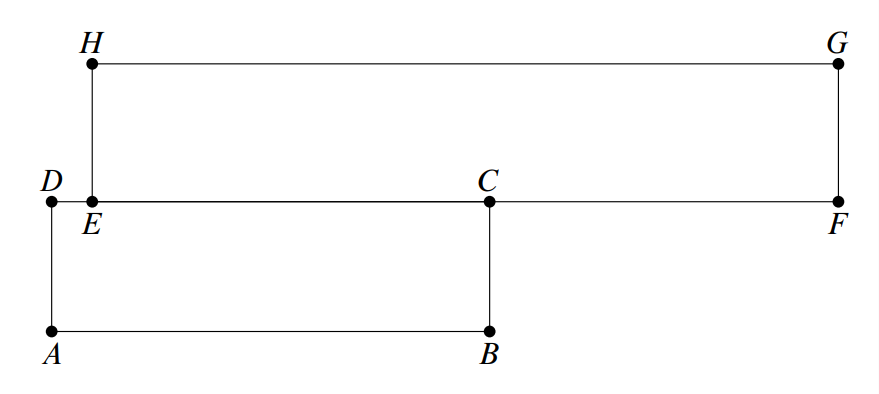
Problem:
Rectangle ABCD has dimensions AB=107 and BC=16, and rectangle EFGH has dimensions EF=184 and FG=17. Points D,E,C, and F lie on line DF in that order, and A and H lie on opposite sides of line DF, as shown. Points A,D,H, and G lie on a common circle. Find CE.
Solution:
Let W be the intersection of lines GH and AD. Let z=DE. Then the power of the point W with respect to the circle passing through A,D,H, and G is WD⋅WA=WH⋅WG, so 17⋅(17+16)=z(z+184), which simplifies to
0=z2+184z−561=(z+187)(z−3).
Thus z=3, and the requested distance is CE=107−z=104.
OR
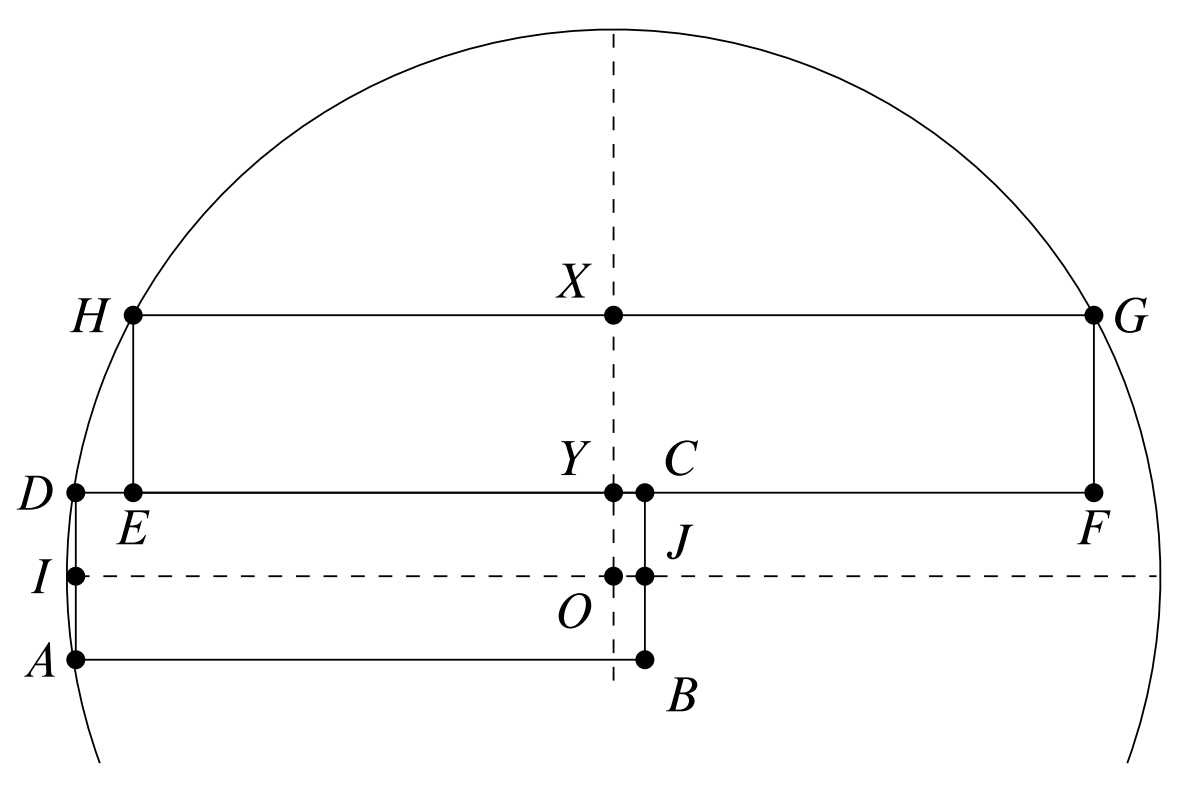
Let I,J,X, and Y be the midpoints of AD,BC,GH, and EF, respectively, and let O be the center of the circle circumscribing ADHG. Then lines IJ and XY intersect at point O, as shown.
Then DI=8,OX=25, and HX=92. Let x=CE. Then DE=CD−x=107−x, and
OI=HX+DE=199−x.
Applying the Pythagorean Theorem to right triangles △OID and △OXH gives
OD2=(199−x)2+82andOH2=252+922.
The lengths of OD and OH are equal because they are radii of the same circle. Hence
(199−x)2=922−82+252=(92−8)(92+8)+252=336⋅25+252=25⋅361=52⋅192=952.
The length x must be less than CD, which is given to be 107, so 199−x is a positive real number. Thus 199−x=95, and x=199−95=104.
OR
Let x=CE. Because quadrilateral ADHG is cyclic, ∠ADH and ∠AGH are supplementary. Let W be the intersection of lines AD and GH. Then △AGW∼△DHE, so EHDE=WGAW, which implies
17107−x=184+107−x33=291−x33.
Thus (107−x)(291−x)=17⋅33. Substituting y=199−x yields (y−92)(y+92)=561, so y=95. The requested distance is
CE=x=199−y=199−95=104.
The problems on this page are the property of the MAA's American Mathematics Competitions