¶ 2024 AIME I Problem 6
Problem:
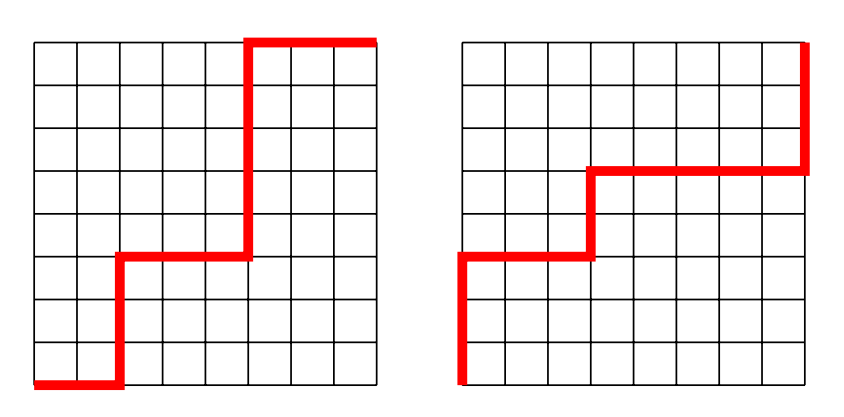
Consider the paths of length that follow the lines from the lower left corner to the upper right corner on an grid. Find the number of such paths that change direction exactly four times, as in the examples shown below.
Solution:
Any such path must consist of steps to the right and steps upward in some order. First consider those paths whose first step is to the right. All such paths start and end with a horizontal segment and include two vertical segments with a horizontal segment in between. The path is completely determined by the choice of the positions of the two vertical segments and the height of the middle horizontal segment. There are ways to select the positions of the two vertical segments and ways to select the height of the middle horizontal segment. Thus there are paths that begin with a horizontal step. By symmetry, there are also paths that begin with a vertical step, so the total number of paths is .
The problems on this page are the property of the MAA's American Mathematics Competitions