¶ 2024 AIME I Problem 8
Problem:
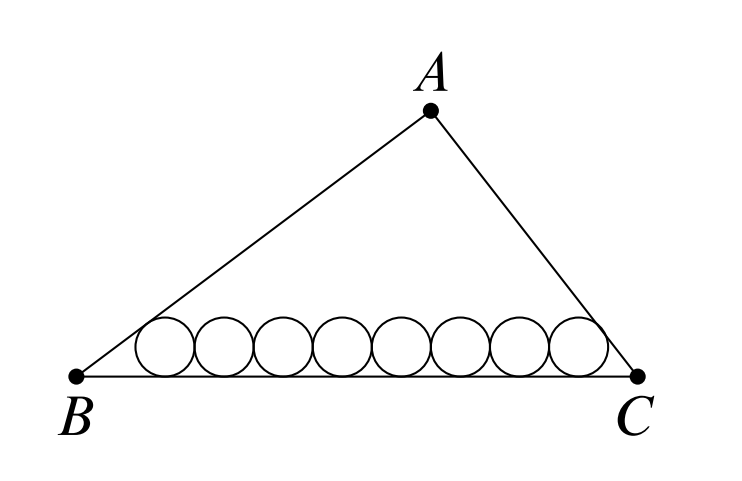
Eight circles of radius can be placed tangent to side of so that the circles are sequentially tangent to each other, with the first circle being tangent to and the last circle being tangent to , as shown. Similarly, circles of radius can be placed tangent to in the same manner. The inradius of can be expressed as , where and are relatively prime positive integers. Find .
Solution:
Let be the incenter of , and let be its inradius, which is the height of from to . If there are circles of radius tangent to and tangent to each other in a line, then the distance between the centers of the first and last circles is . For the first and last circles to be tangent to and , respectively, the first circle's center must lie on , and the last circle's center must lie on .
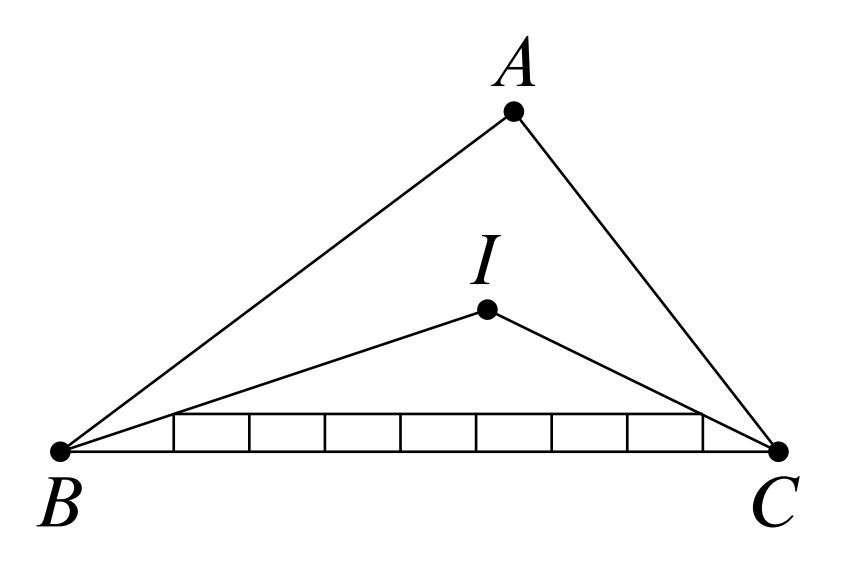
This implies that contains an inscribed rectangle with dimensions by with its longer side along , as well as an inscribed rectangle with dimensions by with its longer side along . There are two similar triangles each with two sides along and and a third side that is a side of one of these two inscribed rectangles. Because similar triangles have altitudes with the same ratio as the ratios of their side lengths,
Solving this equation gives . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions