¶ 2024 AIME I Problem 9
Problem:
Let and be points on the hyperbola such that is a rhombus whose diagonals intersect at the origin. Find the greatest real number that is less than for all such rhombi.
Solution:
Without loss of generality, let diagonal have positive slope , with having positive coordinates, as in the diagram. Because the diagonals of a rhombus are perpendicular, line has slope . If the lines and each intersect the hyperbola in two points ( and , respectively), then is indeed a rhombus, because symmetry of the hyperbola about the origin implies that and bisect each other.
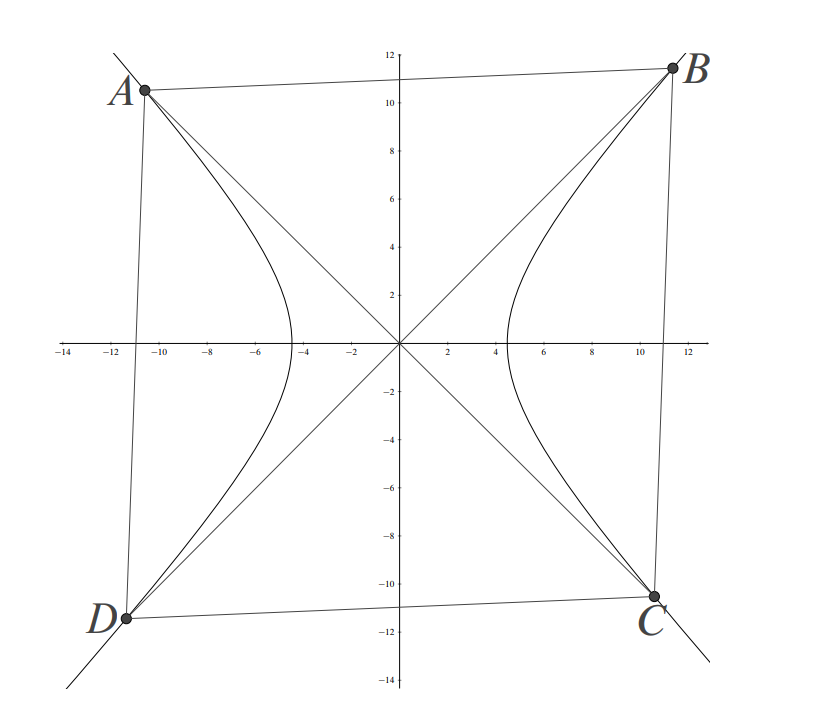
The asymptotes of the hyperbola have slopes , so the necessary intersections occur if both and are less than , which is equivalent to . From the diagram, note that as decreases, the distance from the origin to decreases, and hence so does . Therefore the desired lower bound equals the square of the length of the segment between intersection points of the hyperbola with the line passing through the origin that is perpendicular to the negatively sloped asymptote of the hyperbola, as shown in the diagram below.
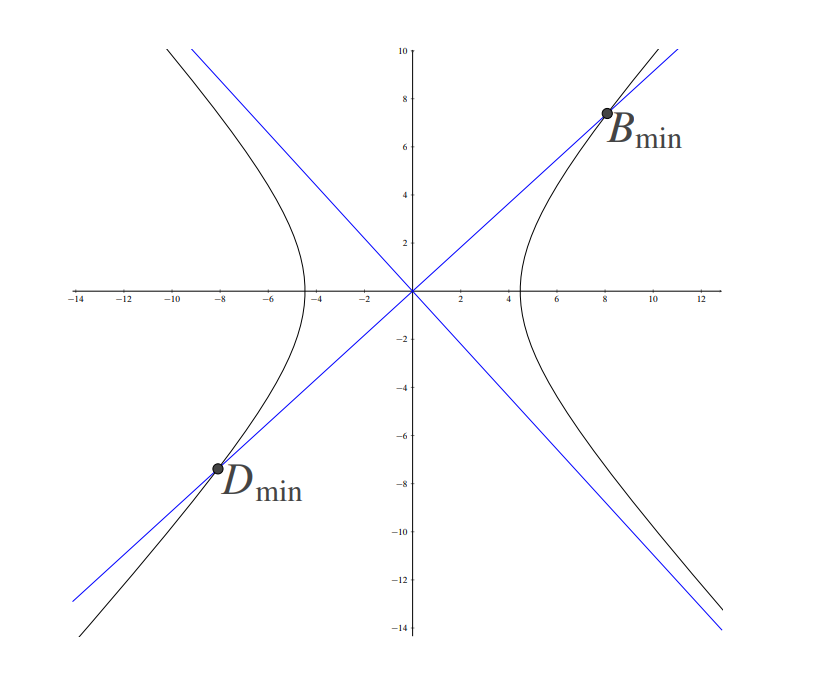
The line perpendicular to the asymptote has the equation , which intersects the hyperbola at points and , respectively. The requested square of the distance between these two points is
The problems on this page are the property of the MAA's American Mathematics Competitions