¶ 2024 AIME II Problem 1
Problem:
Among the residents of Aimeville, there are who own a diamond ring, who own a set of golf clubs, and who own a garden spade. In addition, each of the residents owns a bag of candy hearts. There are residents who own exactly two of these things, and residents who own exactly three of these things. Find the number of residents of Aimeville who own all four of these things.
Solution:
Let be the number of people owning all four items, and let be the number of people owning only a bag of candy hearts. Then the total number of instances of a resident owning something is given by . Also . Thus
from which .
The following Venn diagram shows that such a situation is possible.
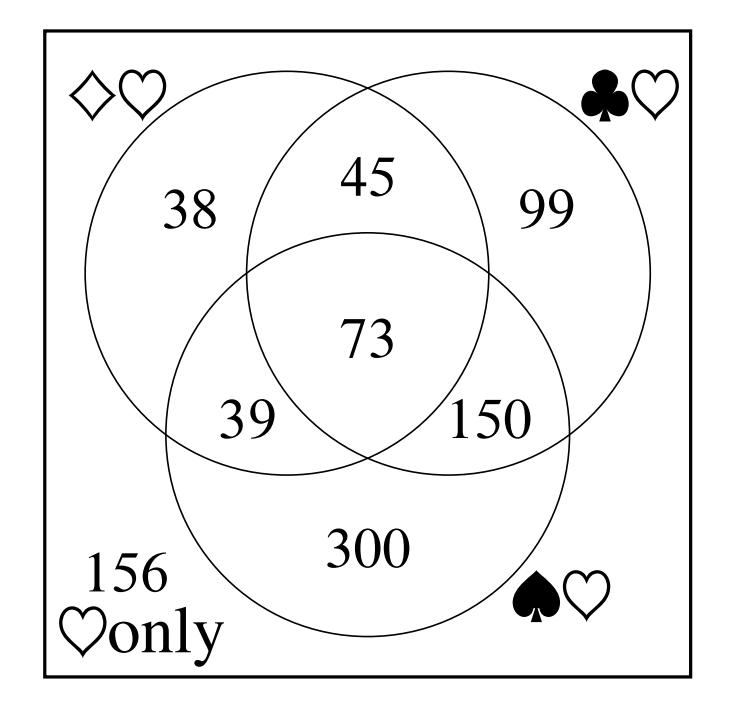
Let be the number of residents who own all four things. Then the number of residents who own diamond rings plus the number of residents who own golf clubs plus the number of residents who own garden spades counts the residents who own exactly three of the four things twice and the residents who own all four things three times. Thus the number of residents who own exactly two things can be calculated as
Solving this equation gives . The fact that there are residents in all is irrelevant.
The problems on this page are the property of the MAA's American Mathematics Competitions