¶ 2024 AIME II Problem 15
Problem:
Find the number of rectangles inside a fixed regular dodecagon (-gon) where each side of the rectangle lies on a side or on a diagonal of the dodecagon. The diagram below shows three of those rectangles
Solution:
In what follows, the word "diagonal" means "diagonal or side of the dodecagon", and "parallel" is used in the inclusive sense where a line (or segment) is thought of as being parallel to itself.
Let be the regular dodecagon. Any rectangle whose sides lie along the diagonals of this -gon must have one pair of sides parallel to one of the segments or .
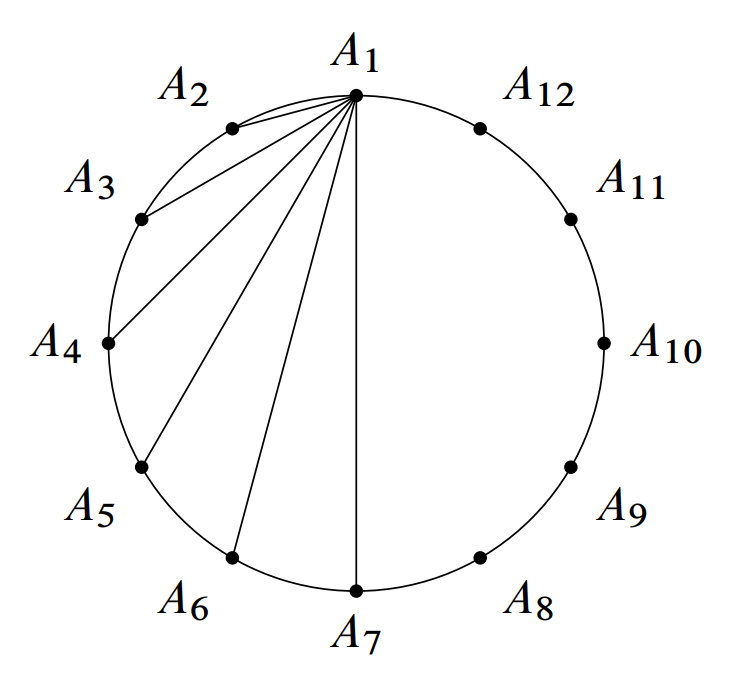
For each of the diagonals and , there are other diagonals of the dodecagon parallel to it. For the other three diagonals, and , there are other diagonals parallel to it, as shown in the examples below.
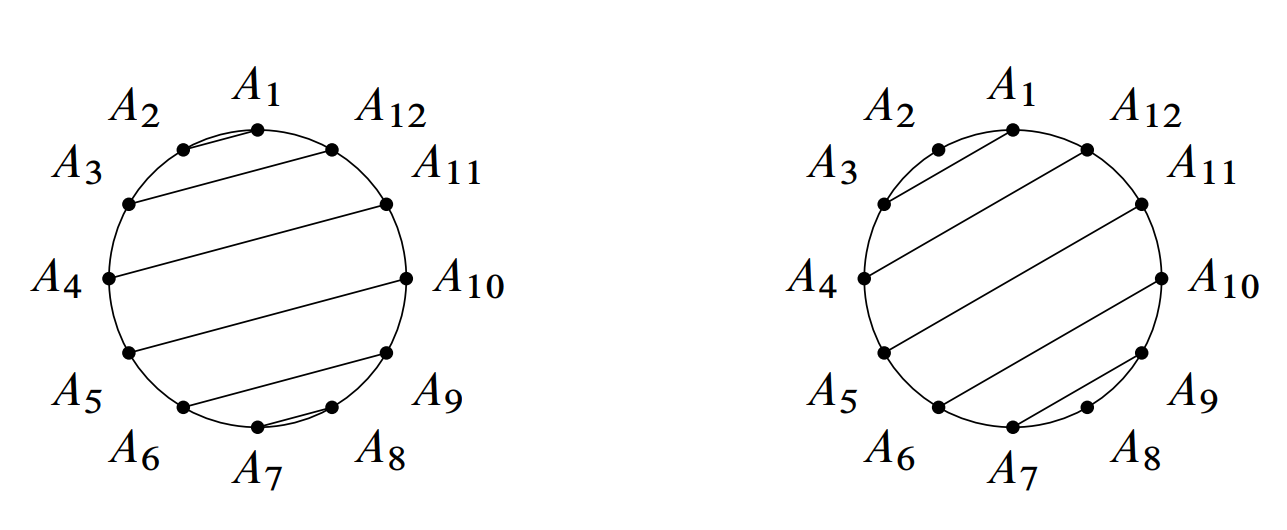
Consider the case of rectangles with sides parallel to . The two sides of the rectangle parallel to lie along of possible diagonals, so there are possible pairs of diagonals.
- If the shorter of these two diagonals has length ( of the pairs), there are only possible diagonals perpendicular to for the other two sides of the rectangle, and thus there is only choice for those sides.
- If the shorter of these two diagonals has length ( of the pairs), there are possible diagonals perpendicular to for the other two sides of the rectangle, and thus there are choices for those sides.
- If the shorter of these two diagonals has length ( of the pairs), there are possible diagonals perpendicular to for the other two sides of the rectangle, and thus there are choices for those sides.
Therefore there are rectangles with two sides parallel to . Similarly, there are rectangles with sides parallel to and with sides parallel to for a total of rectangles in this case.
Consider the case of rectangles with sides parallel to . The two sides of the rectangle parallel to lie along of possible diagonals, so there are possible pairs of diagonals.
- If the shorter of these two diagonals has length ( of the pairs), there are possible diagonals perpendicular to for the other two sides of the rectangle, and thus there are choices for those sides.
- If the shorter of these two diagonals has length ( of the pairs), there are possible diagonals perpendicular to for the other two sides of the rectangle, and thus there are choices for those sides.
Therefore there are rectangles with two sides parallel to . Similarly, there are rectangles with sides parallel to and with sides parallel to for a total of rectangles in this case.
The total number of rectangles is .
Let be the regular dodecagon, and consider a rectangle whose edges lie on and for some
as shown in the next diagram.
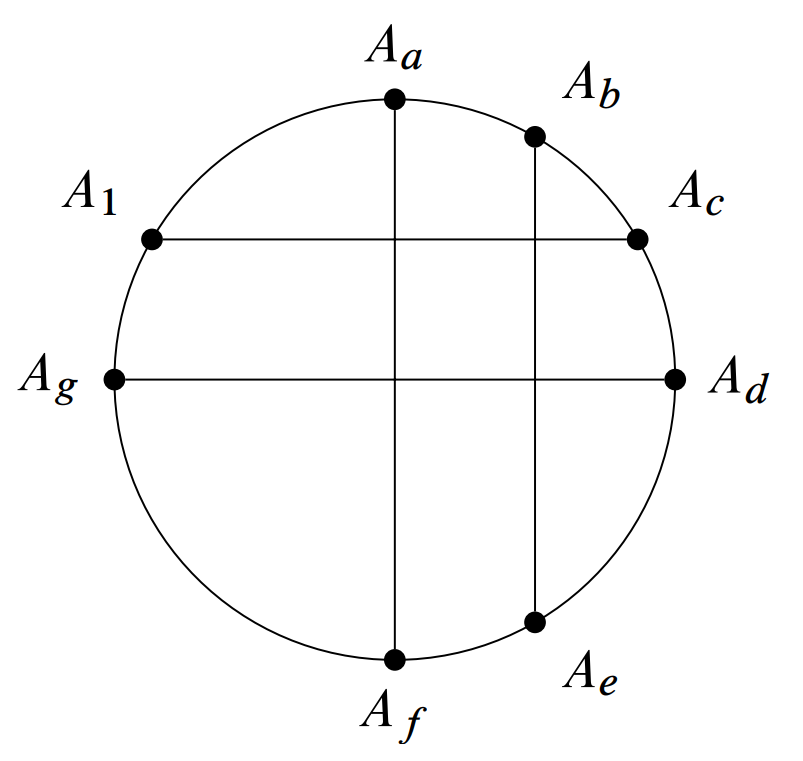
Because opposite sides are parallel, it must be that and for some . Let . Because
it must be that .
Let and so that for all . In order for to be perpendicular to , it must be that
so that and similarly .
To select a rectangle, first choose satisfying and note that
- there are choices for and such that ;
- there are choices for and such that ;
- and likewise there are choices for and .
There are therefore
of these rectangles.
This count was done starting with the location of , but the count could have been done by starting with any of the vertices. Because each rectangle has sides, multiplying the above count of by would overcount by a factor of . It follows that the total number of rectangles is .
The problems on this page are the property of the MAA's American Mathematics Competitions