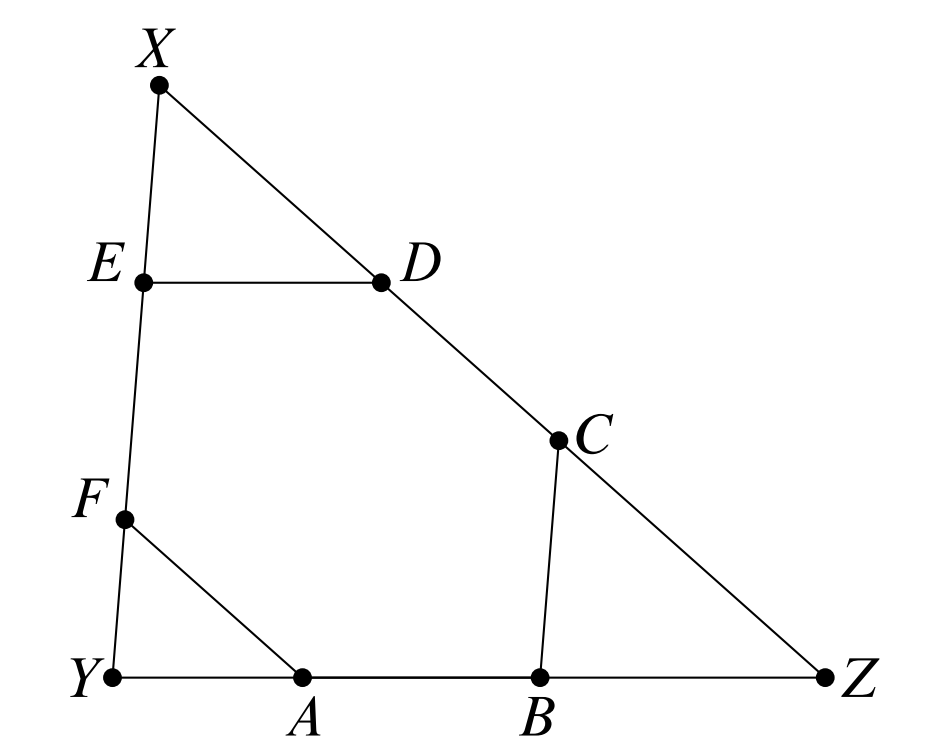
Problem:
Let ABCDEF be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments AB,CD, and EF has side lengths 200,240, and 300. Find the side length of the hexagon.
Solution:
Suppose that lines AB,CD, and EF bound ΞXYZ, as shown. Let s be the side length of the hexagon.
Observe that triangles ΞXED,ΞFYA, and ΞCBZ are similar to ΞXYZ with ratios YZsβ,ZXsβ, and XYsβ, respectively. Thus
YZ=YA+AB+BZ=YZβ
ZXsβ+YZβ
YZsβ+YZβ
XYsβ.
It follows that
ZXsβ+YZsβ+XYsβ=1,
so
s1β=ZX1β+YZ1β+XY1β=2001β+2401β+3001β=12006+5+4β=801β.
Therefore the requested side length is s=80β.
The problems on this page are the property of the MAA's American Mathematics Competitions
