¶ 2024 AIME II Problem 8
Problem:
Torus is the surface produced by revolving a circle with radius around an axis in the plane of the circle that is a distance from the center of the circle.
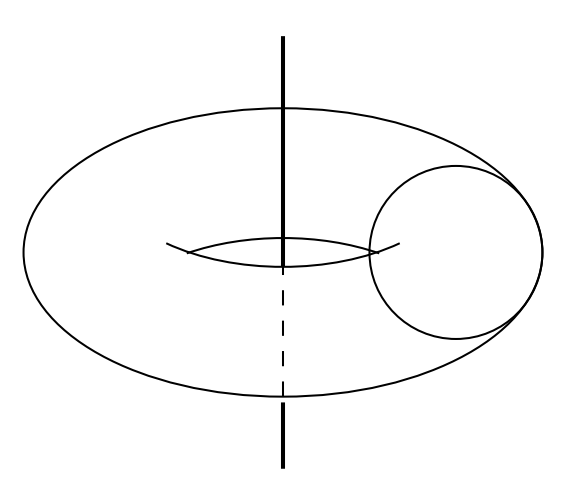
Let be a sphere with radius . When rests on the inside of , it is internally tangent to along a circle with radius , and when rests on the outside of , it is externally tangent to along a circle with radius . The difference can be written as , where and are relatively prime positive integers. Find .
Solution:
More generally, let the sphere have radius , and let the torus be the locus of points a distance from a circle with radius , where . Let one copy of rest on the inside of and a second copy rest on the outside of . Consider a cross section of these copies of and containing the centers of the three figures, as shown.
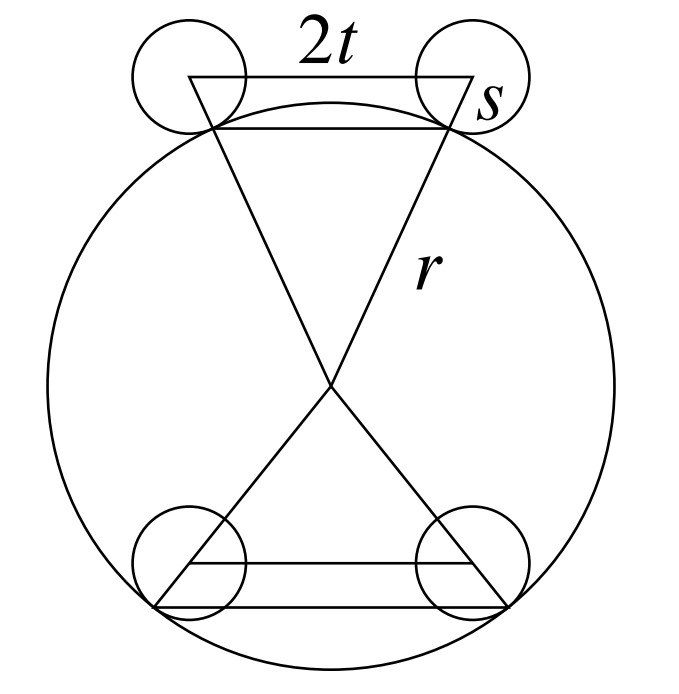
By similar triangles , so . Also by similar triangles , so . The required difference is
In the given problem where and , the required difference is . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions