¶ 2025 AIME I Problem 10
Problem:
The cells of a grid are filled in using the numbers through so that each row contains different numbers, and each of the three blocks heavily outlined in the example below contains different numbers, as in the first three rows of a Sudoku puzzle.
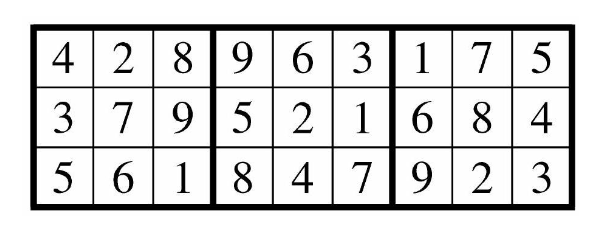
The number of different ways to fill such a grid can be written as , where and are distinct prime numbers and and are positive integers. Find .
Solution:
WLOG, let the numbers in the first grid be through filled in sorted order left to right then top to bottom. Now we count the number of ways to pick which numbers end up in which row of the second grid. Case on how many of the numbers in the first row of the second grid come from :
Case 1: numbers
The numbers must go in the second row and must be in the third.
Case 2: numbers
There are ways to pick two numbers from to be in the top row and ways to pick the number from . The remaining two numbers from must go in the third row with one of numbers selected from the first row. This gives a total of possibilities for this case.
Case 3: number
This case is symmetric to Case 2 for possibilities.
Case 4: numbers
This case is symmetric to Case 1 for possibility.
In total there are ways to pick the set of numbers for each row in the second grid. Note that the set of numbers for each row in the third grid are now fixed. All that is left to do is to order the numbers in each row of the second and third grids. This gives a final count of:
for an answer of .
The problems on this page are the property of the MAA's American Mathematics Competitions