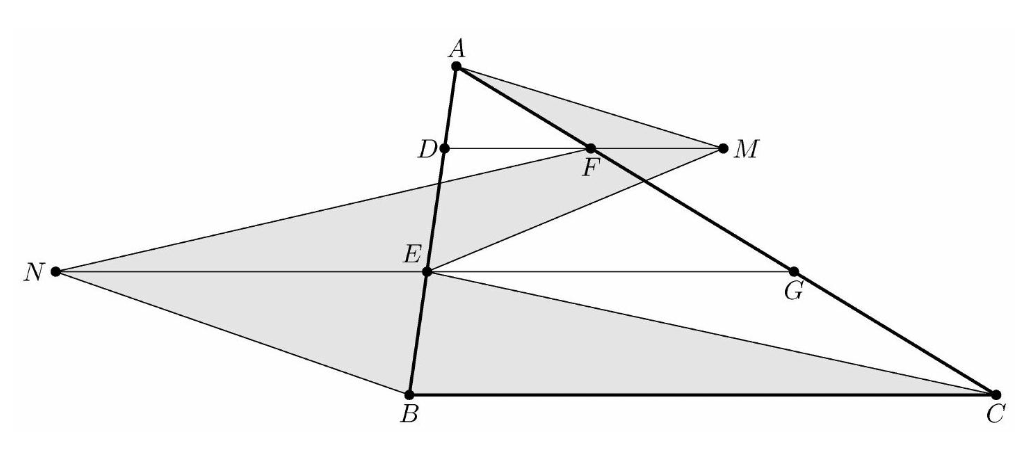
Problem:
On △ABC points A,D,E, and B lie in that order on side AB with AD=4, DE=16, and EB=8. Points A,F,G, and C lie in that order on side AC with AF=13, FG=52, and GC=26. Let M be the reflection of D through F, and let N be the reflection of G through E. Quadrilateral DEGF has area 288. Find the area of heptagon AFNBCEM.
Solution:
Since, ADAF=AEAG=ABAC=413, by SAS similarity, we have that △ADF∼△AEG∼△ABC, and it follows that DF∥EG∥BC.
Break up the shaded region into 5 parts:
[AFNBCEM]=[△AFM]+[△EFM]+[△FEN]+[△BEN]+[△EBC]
Since DF=FM and both triangles share a height from A, [△AFM]=[△ADF].
Similarly, [△EFM]=[△EDF].
From NE=EG, we get [△FEN]=[△FEG].
Similarly, [△BEN]=[△BEG].
Lastly, we have [△EBC]=[△GBC].
Using our equations:
[AFNBCEM]=[△ADF]+[△EDF]+[△FEG]+[△BEG]+[△GBC]=[△ABC]
From AE=5AD and similar triangles,
[△AEG]=25[△ADF]→[DFGE]=24[△ADF]→[△ADF]=24288=12
Since AB=7∗AD,
[△ABC]=49∗[△ADF]=588
The problems on this page are the property of the MAA's American Mathematics Competitions