¶ 2026 AIME I Problem 15
¶ Problem:
Let , , and be positive integers with both and greater than or equal to and less than or equal to . Define an cell loop in a grid of cells to be the cells that surround an (possibly empty) rectangle of cells in the grid. For example, the following diagram shows a way to partition a grid of cells into cell loops.
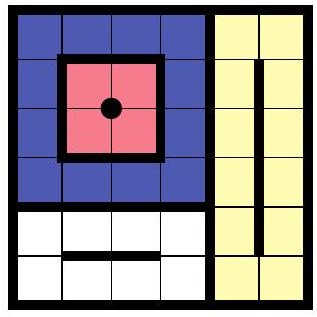
Find the number of ways to partition a grid of cells into cell loops so that every cell of the grid belongs to exactly one cell loop.
¶ Solution:
First, we claim that the minimum number of loops required to tile a grid with is . To fix convention, we will say a grid has rows and columns. Suppose that it is possible to tile the grid with loops. Note that for every row, there must be a loop whose top or bottom edge is in the row. If no edge is in the row, then every loop can cover at most of those rows cells, so loops are required. Since every row has a top or bottom edge of a loop, we require at least loops.
Furthermore, we claim that if , and we are tiling the grid with loops, the loop covering the bottom-left cell must pass through a cell on the right border of the rectangle. If it doesn't, then there are still rows left for which a top or bottom row of a loop must pass through. Any set of loops which cover these rows will be unable to pass through the bottom right cell, leaving it uncovered. Additionally, we note that the bottom left loop must leave an even number of uncovered rows both inside the loop and outside the loop. This is because any future loop may no longer cover both a row above and a row below the top edge of the first loop. If , a similar argument shows that the loop passing through the bottom left cell must either touch the top or right boundary at a distance leaving an even number of rows/columns on each side.
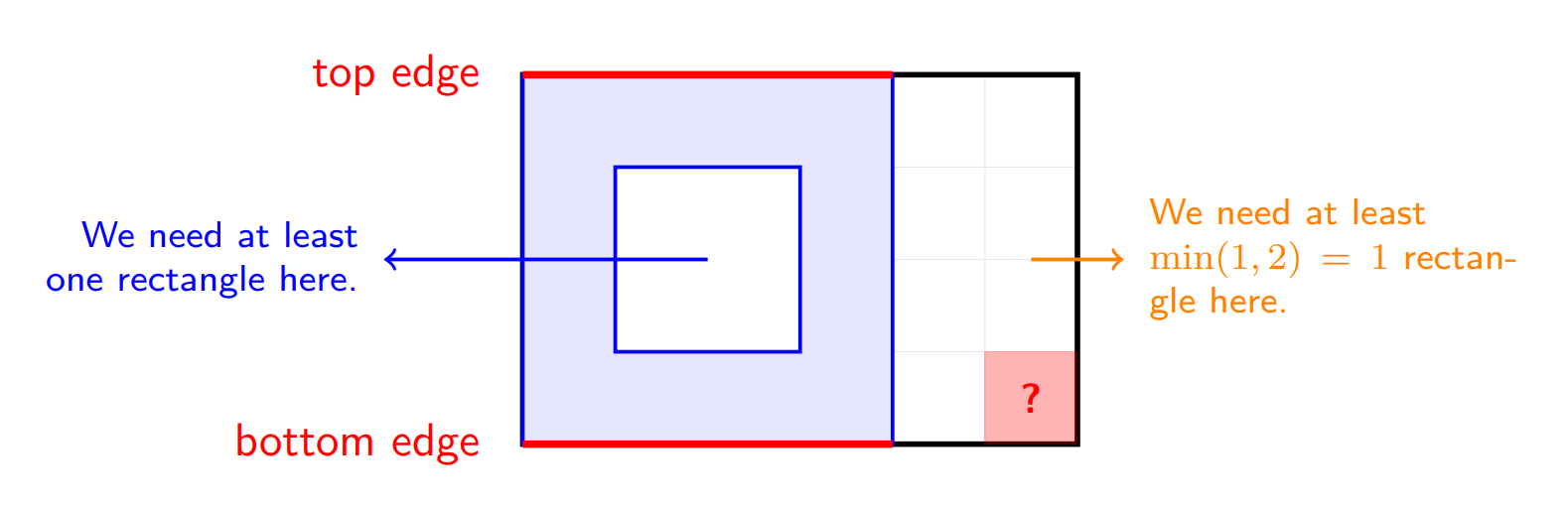
We may put the above observations together to form a full characterization of all loop partitions of a grid. WLOG, suppose the bottom left loop touches the right side. The two rectangles split into must obey the above rules recursively. So, now consider the rows covered by each loop. For two loops and , suppose and refer to the top and bottom rows covered by loop and similarly and for for . It is impossible to have as the loops would then intersect. Every loop must either be disjoint form or fully contain every other loop. We notice that this bijects to balanced parentheses sequences - each can be thought of as a and each as a for every loop. It is well-known that the number of these sequences of length is the th Catalan number.
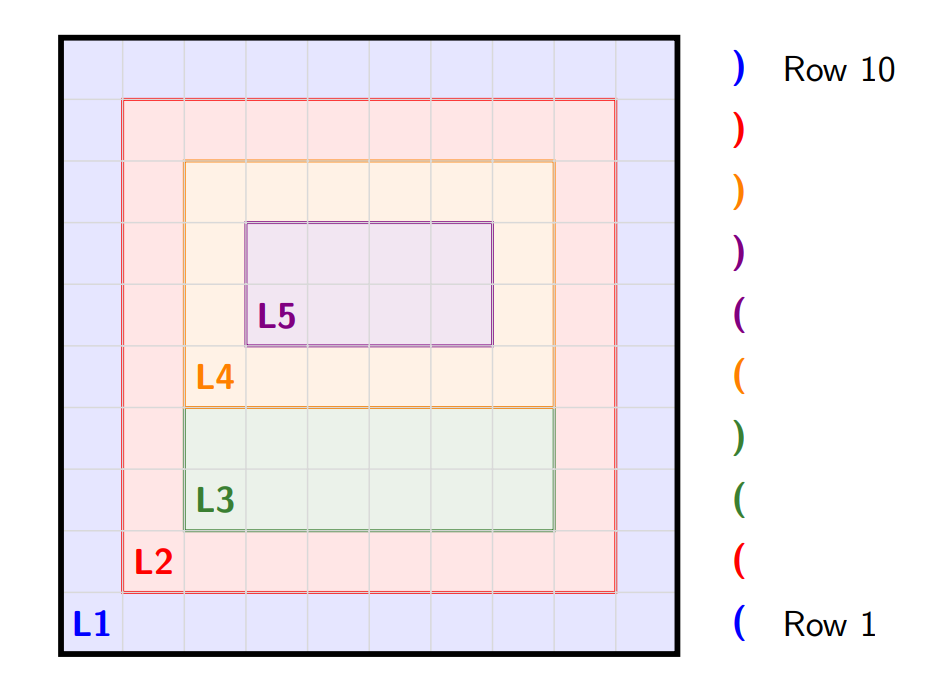
The sequence could possibly lead to this grid, or the rotational equivalent. This particular grid is the horizontal case, as all rectangles are wider than they are tall.
Our count for the catalan number is almost sound - but the way we construct it, we assumed that , meaning that our rectangles will always have larger width than height. The equivalent vertical case can be found by just rotating the entire diagram by , doubling our count. However, these two cases intersect when all rectangles are as tall as they are wide - or we have squares (which is the concentric case). The final answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions