¶ 2026 AIME I Problem 3
¶ Problem:
A hemisphere with radius sits on top of a horizontal circular disk with radius , and the hemisphere and disk have the same center. Let be the region of points in the disk such that a sphere of radius can be placed on top of the disk at and lie completely inside the hemisphere. The area of divided by the area of the disk is , where and are relatively prime positive integers. Find .
¶ Solution:
Consider a random point on the disk, a distance from the center of the disk. The sphere of radius will be centered at a point that is
away from the origin, which we take as the center of the disk.
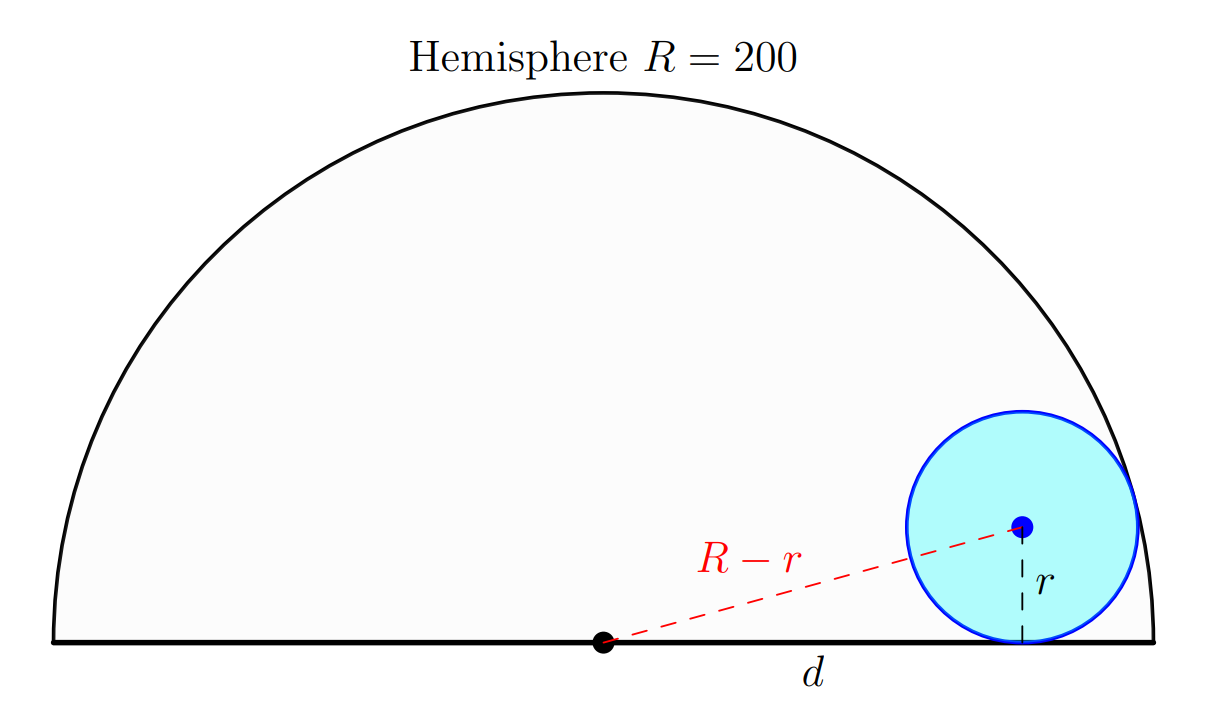
To make sure it fits inside the hemisphere, the furthest point on the sphere can be no further than from the origin. But the Triangle Inequality states that the furthest point on the sphere is the point that lies on the line connecting the origin to the center of the sphere - whose distance is
Thus, we get
This area describes a circle with radius , or an area of . Since our original disk has an area of , our answer is
for an answer of .
The problems on this page are the property of the MAA's American Mathematics Competitions