¶ 2004 AMC 10A Problem 22
Problem:
Square has side length . A semicircle with diameter is constructed inside the square, and the tangent to the semicircle from intersects side at . What is the length of
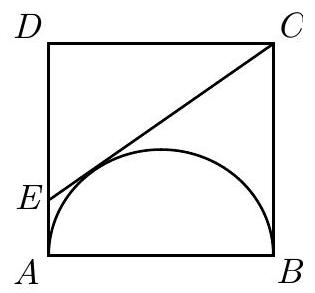
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the point at which is tangent to the semicircle, and let be the midpoint of . Because and are both tangents to the semicircle, . Similarly, . Let . The Pythagorean Theorem applied to gives
It follows that and .
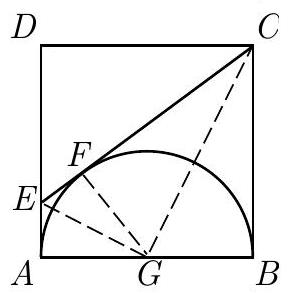
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions