¶ 2004 AMC 10B Problem 16
Problem:
Three circles of radius are externally tangent to each other and internally tangent to a larger circle. What is the radius of the large circle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the center of the large circle, let be the center of one of the small circles, and let and be tangent to the small circle at and .
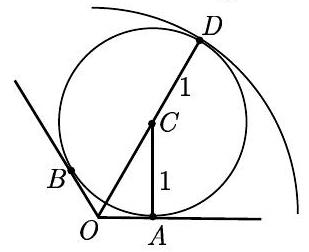
By symmetry, and . Thus is a degree right triangle, and , so
If is a radius of the large circle through , then
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions