¶ 2004 AMC 10B Problem 25
Problem:
A circle of radius is internally tangent to two circles of radius at points and , where is a diameter of the smaller circle. What is the area of the region, shaded in the picture, that is outside the smaller circle and inside each of the two larger circles?
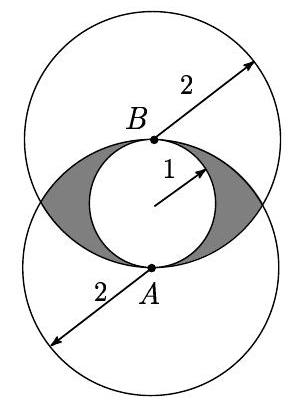
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The centers of the two larger circles are at and . Let be the center of the smaller circle, and let be one of the points of intersection of the two larger circles.
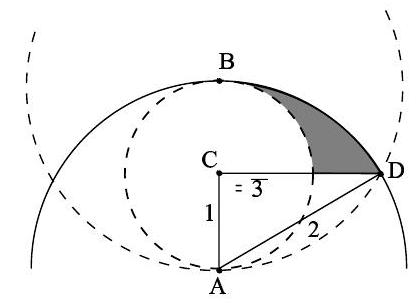
Then is a right triangle with and , so , , and the area of is . The area of of the shaded region, as shown in the Figure, is the area of sector of the circle centered at , minus the area of , minus the area of of the smaller circle. That area is
so the area of the entire shaded region is
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions