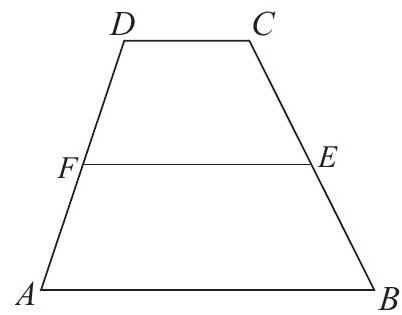
Problem:
In trapezoid ABCD we have AB parallel to DC,E as the midpoint of BC, and F as the midpoint of DA. The area of ABEF is twice the area of FECD. What is AB/DC?
Answer Choices:
A. 2
B. 3
C. 5
D. 6
E. 8
Solution:
First note that FE=(AB+DC)/2. Because trapezoids ABEF and FECD have the same height, the ratio of their areas is equal to the ratio of the averages of their parallel sides. Since
AB+2AB+DC=23AB+DC
and
2AB+DC+DC=2AB+3DC
we have
3AB+DC=2(AB+3DC)=2AB+6DC, and DCAB=5
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions