Problem:
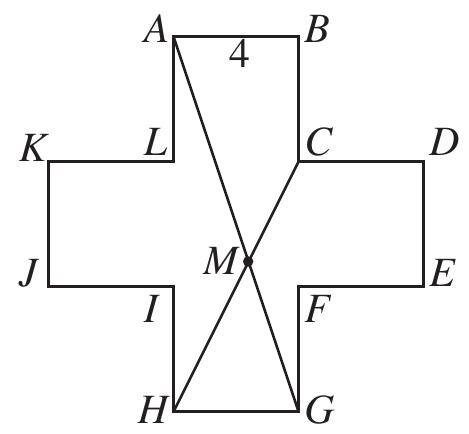
Consider the 12-sided polygon ABCDEFGHIJKL, as shown. Each of its sides has length 4, and each two consecutive sides form a right angle. Suppose that AG and CH meet at M. What is the area of quadrilateral ABCM?
Answer Choices:
A. 344
B. 16
C. 588
D. 20
E. 362
Solution:
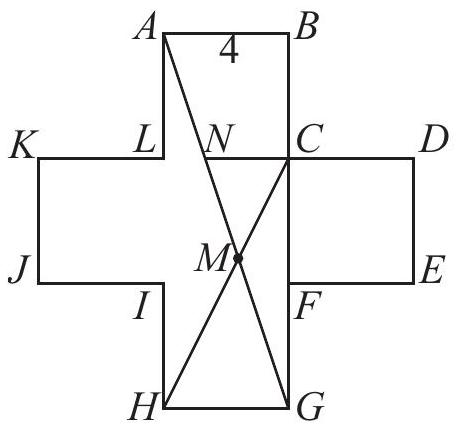
Extend CD past C to meet AG at N.
Since △ABG is similar to △NCG,
NC=AB⋅BGCG=4⋅128=38
This implies that trapezoid ABCN has area
21⋅(38+4)⋅4=340
Let v denote the length of the perpendicular from M to NC. Since △CMN is similar to △HMG, and
NCGH=8/34=23
the length of the perpendicular from M to HG is 23v. Because
v+23v=8, we have v=516
Hence the area of △CMN is
21⋅38⋅516=1564
So
Area(ABCM)=Area(ABCN)+Area(△CMN)=340+1564=(C)588
OR
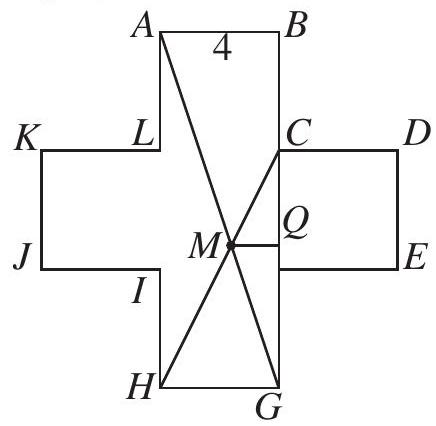
Let Q be the foot of the perpendicular from M to BG.
Since △MQG is similar to △ABG, we have
QGMQ=BGAB=124=31
Also, △MCQ is similar to △HCG, so
CQMQ=CGHG=84=21
Thus
QG=3MQ=3(21CQ)=23(8−QG),
which implies that
QG=524 and MQ=31QG=58.
Hence
Area(ABCM)=Area(△ABG)−Area(△CMG)=21⋅4⋅12−21⋅8⋅58=(C)588
The problems on this page are the property of the MAA's American Mathematics Competitions