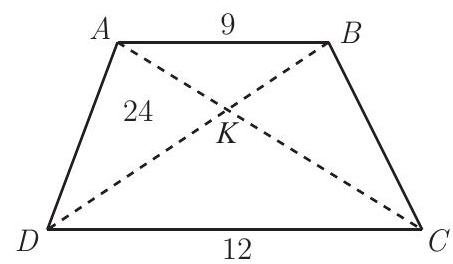
Problem:
Trapezoid ABCD has bases AB and CD and diagonals intersecting at K. Suppose that AB=9,DC=12, and the area of △AKD is 24. What is the area of trapezoid ABCD?
Answer Choices:
A. 92
B. 94
C. 96
D. 98
E. 100
Solution:
Note that △ABK is similar to △CDK. Because △AKD and △KCD have collinear bases and share a vertex D,
Area(△AKD)Area(△KCD)=AKKC=ABCD=34
so △KCD has area 32.
By a similar argument, △KAB has area 18. Finally, △BKC has the same area as △AKD since they are in the same proportion to each of the other two triangles. The total area is 24+32+18+24=(D)98.
OR
Let h denote the height of the trapezoid. Then
24+Area(△AKB)=29h
Because △CKD is similar to △AKB with similarity ratio 912=34,
Area(△CKD)=916Area(△AKB), so 24+916Area(△AKB)=212h.
Solving the two equations simultaneously yields h=328. This implies that the area of the trapezoid is
21⋅328(9+12)=(D)98
The problems on this page are the property of the MAA's American Mathematics Competitions