Problem:
Quadrilateral ABCD has AB=BC=CD,β ABC=70β, and β BCD=170β. What is the degree measure of β BAD?
Answer Choices:
A. 75
B. 80
C. 85
D. 90
E. 95
Solution:
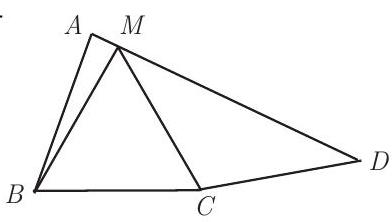
Let M be on the same side of line BC as A, such that β³BMC is equilateral. Then β³ABM and β³MCD are isosceles with β ABM=10β and β MCD= 110β. Hence β AMB=85β and β CMD=35β. Therefore
β AMDβ=360βββ AMBββ BMCββ CMD=360ββ85ββ60ββ35β=180β.β
It follows that M lies on AD and β BAD=β BAM=(C)85ββ.
OR
Let β³ABO be equilateral as shown.
Then
β OBC=β ABCββ ABO=70ββ60β=10β.
Because β BCD=170β and OB=BC=CD, the quadrilateral BCDO is a parallelogram. Thus
OD=BC=AO and β³AOD is isosceles. Let Ξ±=β ODA=β OAD. The sum of the interior angles of ABCD is 360β, so we have
360=(Ξ±+60)+70+170+(Ξ±+10) and Ξ±=25.
Thus β DAB=60+Ξ±=(C)85ββ.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)