¶ 2009 AMC 10A Problem 16
Problem:
Let , and be real numbers with , and . What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The given conditions imply that , and , where the signs can be combined in all possible ways. Therefore the possible values of are , , and . The sum of all possible values of is .
The equations in the problem statement are true for numbers if and only if they are true for , where is any real number. The value of is also unchanged with this substitution. Therefore there is no loss of generality in letting , and we can then write down the possibilities for the other variables:
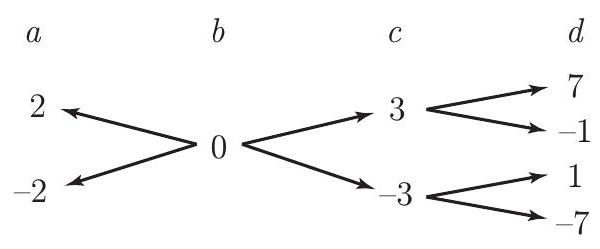
The different possible values for are
The sum of these possible values is .
The problems on this page are the property of the MAA's American Mathematics Competitions