¶ 2009 AMC 10B Problem 16
Problem:
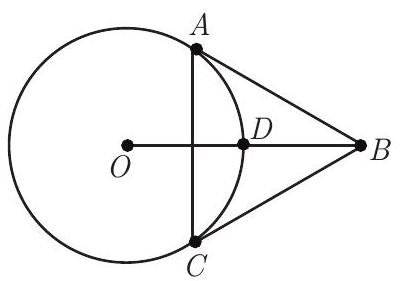
Points and lie on a circle centered at , each of and are tangent to the circle, and is equilateral. The circle intersects at . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the radius of the circle be . Because is a right triangle with a angle at , the hypotenuse is twice as long as , so . It follows that , and
The problems on this page are the property of the MAA's American Mathematics Competitions