¶ 2011 AMC 10A Problem 18
Problem:
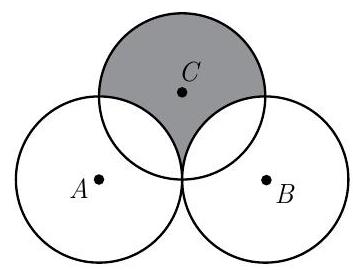
Circles , and each have radius . Circles and share one point of tangency. Circle has a point of tangency with the midpoint of . What is the area inside circle but outside circle and circle ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
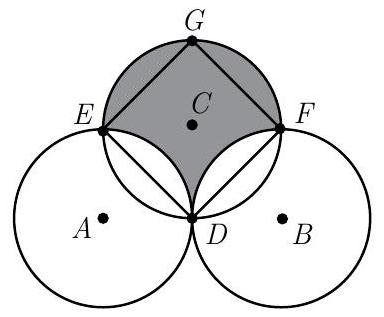
Let be the midpoint of , and let circle intersect circles and at and , respectively, distinct from . The shaded portion of unit square has area , as does the shaded portion of unit square . The portion of the shaded region which is outside these squares is a semicircle of radius and has area . The total shaded area is .
Let , and be defined as in the first solution, and let be diametrically opposite on circle . The shaded area is equal to the area of square , which has diagonal length . Its side length is , and its area is .
The problems on this page are the property of the MAA's American Mathematics Competitions