¶ 2012 AMC 10B Problem 12
Problem:
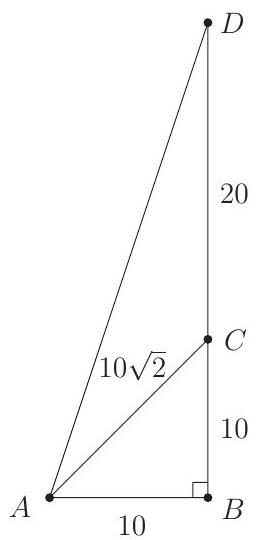
Point is due east of point . Point is due north of point . The distance between points and is meters, and . Point is meters due north of point . The distance is between which two integers?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Note that , so is a triangle. Because hypotenuse , the legs of have length 10. Therefore and . By the Pythagorean Theorem,
Because and , it follows that .
The problems on this page are the property of the MAA's American Mathematics Competitions