¶ 2012 AMC 10B Problem 17
Problem:
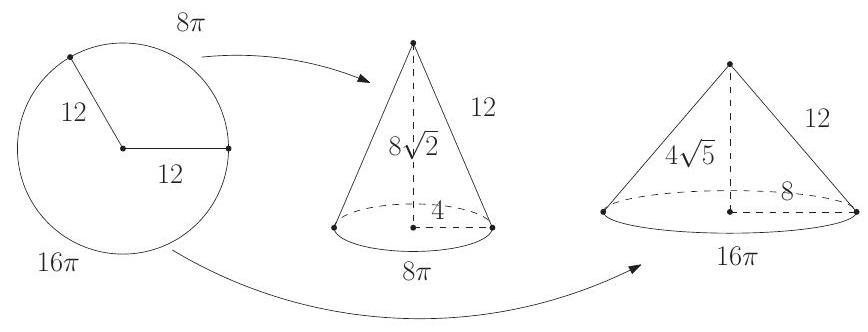
Jesse cuts a circular paper disk of radius along two radii to form two sectors, the smaller having a central angle of degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Each sector forms a cone with slant height . The circumference of the base of the smaller cone is . Hence the radius of the base of the smaller cone is and its height is . Similarly, the circumference of the base of the larger cone is . Hence the radius of the base of the larger cone is and its height is . The ratio of the volume of the smaller cone to the volume of larger cone is
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions