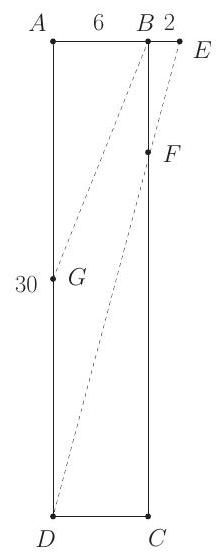
Problem:
In rectangle ABCD,AB=6,AD=30, and G is the midpoint of AD. Segment AB is extended 2 units beyond B to point E, and F is the intersection of ED and BC. What is the area of BFDG?
Answer Choices:
A. 2133
B. 67
C. 2135
D. 68
E. 2137
Solution:
Because △EBF is similar to △EAD, it follows that ADBF=AEBE, or 30BF=82, giving BF=215. The area of trapezoid BFDG is
21h(b1+b2)=21⋅AB⋅(BF+GD)=21⋅6⋅(215+15)=(C)2135.
The problems on this page are the property of the MAA's American Mathematics Competitions