Problem:
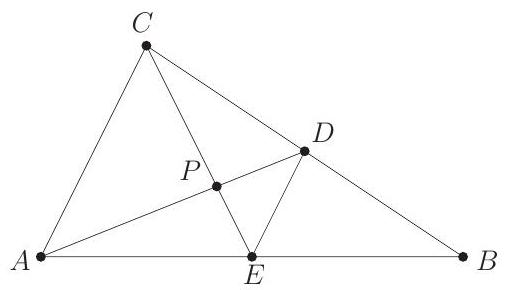
In △ABC, medians AD and CE intersect at P,PE=1.5,PD=2, and DE=2.5. What is the area of AEDC?
Answer Choices:
A. 13
B. 13.5
C. 14
D. 14.5
E. 15
Solution:
The ratio of PE:PD:DE is 3:4:5.
Hence by the converse of the Pythagorean Theorem, △DPE is a right triangle. Therefore CE is perpendicular to AD, and the area of AEDC is one-half the product of its diagonals. Because P is the centroid of △ABC, it follows that CE=3(PE)=4.5 and AD=3(PD)=6. Therefore the area of AEDC is 0.5(4.5)(6)=(B)13.5.
OR
From the first solution, triangles CPD,DPE,EPA, and APC are right triangles with right angle at P. The area of trapezoid AEDC is given by the sum of the areas of these four triangles. Because DE is parallel to AC and D is the midpoint of CB, triangles BAC and BED are similar with common ratio 2, so AC=2⋅DE=5. Triangles APC and DPE are similar, so AP=4 and CP=3. Thus the area of AEDC is
21⋅4⋅1.5+21⋅3⋅4+21⋅2⋅3+21⋅2⋅1.5=(B)13.5
The problems on this page are the property of the MAA's American Mathematics Competitions