¶ 2013 AMC 10B Problem 22
Problem:
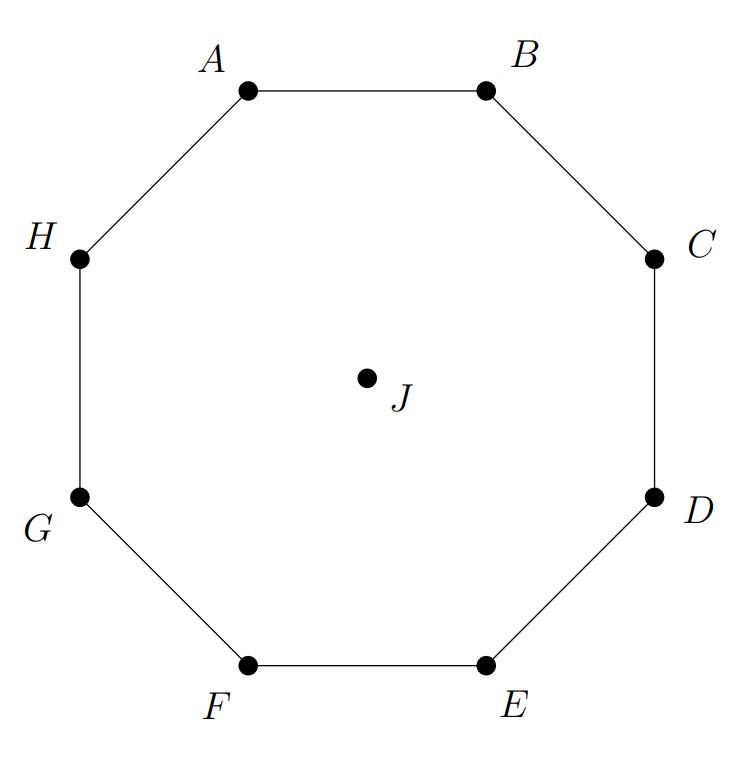
The regular octagon has its center at . Each of the vertices and the center are to be associated with one of the digits through , with each digit used once, in such a way that the sums of the numbers on the lines , , and are equal. In how many ways can this be done?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The digit at contributes to all four sums, and each of the other digits contributes to exactly one sum. Therefore the sum of all four sums is . Because all four sums are equal, this must be a multiple of , so , or . For each choice of , pair up the remaining digits so that each pair has the same sum. For example, for the pairs are and , and , and , and and . Then order the pairs so that they correspond to the vertex pairs . This results in different combinations for each . Thus the requirements can be met in ways.
The problems on this page are the property of the MAA's American Mathematics Competitions