¶ 2014 AMC 10A Problem 16
Problem:
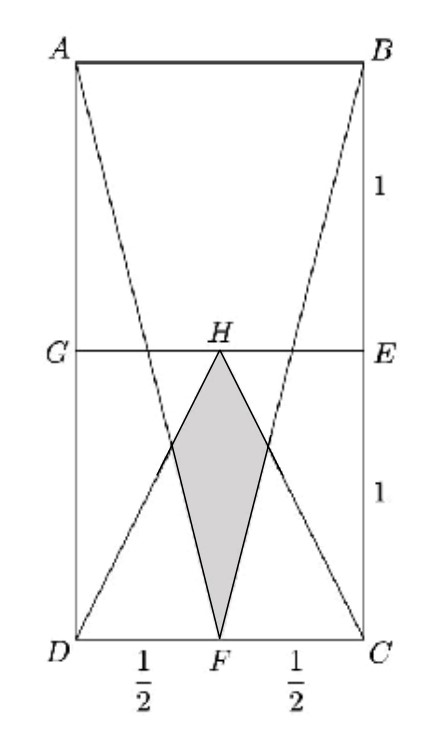
In rectangle , and points , and are midpoints of , and , respectively. Point is the midpoint of . What is the area of the shaded region?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the intersection point of and . Then is similar to with ratio . The length of the altitude of to plus the length of the altitude of to is . Thus has altitude and base , and its area is . The shaded area is twice the area of , or .
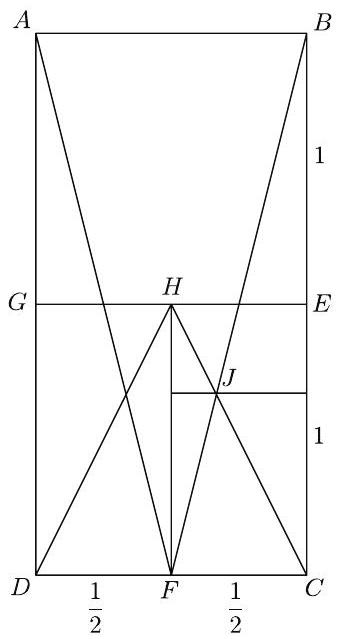
Place the figure on the coordinate plane with at the origin. Then the equation of line is , and the equation of line is . Solving the equations simultaneously shows that the leftmost point of the shaded region has -coordinate . The kite therefore has diagonals and , so its area is .
The problems on this page are the property of the MAA's American Mathematics Competitions