¶ 2015 AMC 10B Problem 19
Problem:
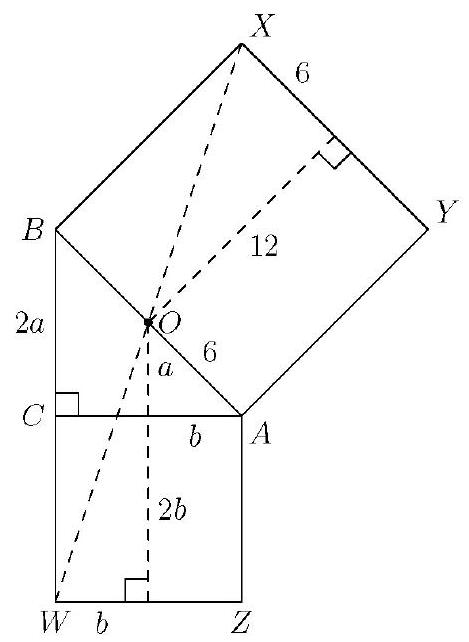
In and . Squares and are constructed outside of the triangle. The points , and lie on a circle. What is the perimeter of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the center of the circle on which , and lie. Then lies on the perpendicular bisectors of segments and , and . Note that segments and have the same perpendicular bisector and segments and have the same perpendicular bisector, from which it follows that lies on the perpendicular bisectors of segments and ; that is, is the circumcenter of . Because is the midpoint of hypotenuse . Let and . Then and . Solving these two equations simultaneously gives . Thus the perimeter of is .
The problems on this page are the property of the MAA's American Mathematics Competitions