¶ 2019 AMC 10A Problem 7
Problem:
Two lines with slopes and intersect at . What is the area of the triangle enclosed by these two lines and the line ?
Answer Choices:
A.
B.
C.
D.
E. 6 \sqrt
Solution:
Let be the intersection point. The two lines have equations and . They intersect at and . Consider to be the base of the triangle; then the altitude of the triangle is the segment joining and . By the Distance Formula, the area of is
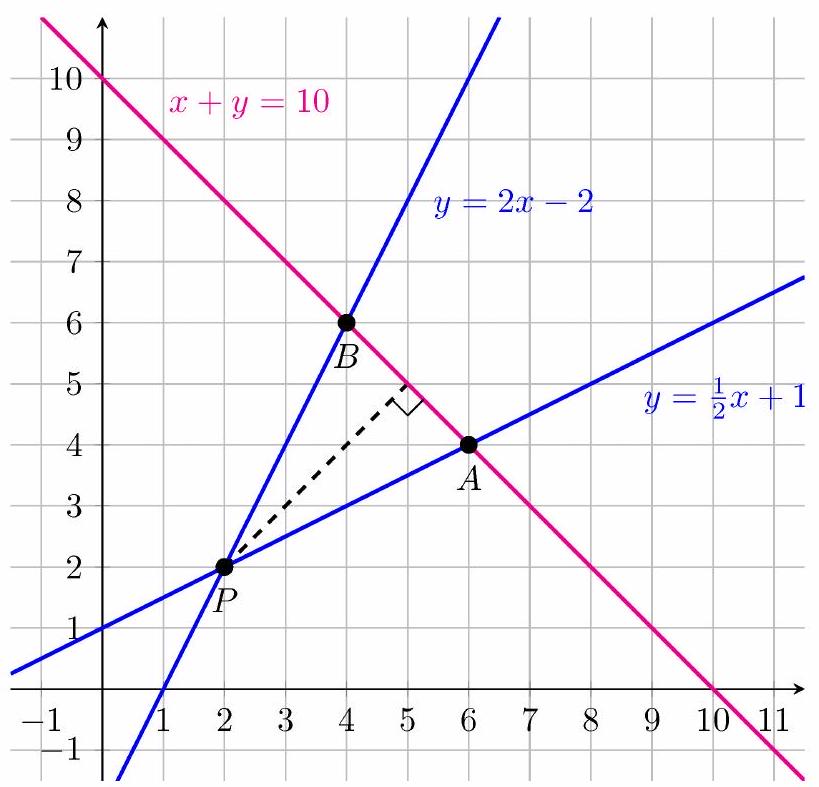
Note: The area of the triangle with vertices , and can be calculated in a number of other ways, such as by enclosing it in a square with sides parallel to the coordinate axes and subtracting the areas of three right triangles; by splitting it into two triangles with the line ; by the shoelace formula:
or by observing that there are lattice points in the interior of the triangle and lattice points on the boundary, and using Pick's Formula: .
The problems on this page are the property of the MAA's American Mathematics Competitions