¶ Spring 2021 AMC 10A Problem 21
Problem:
Let be an equiangular hexagon. The lines , and determine a triangle with area , and the lines , and determine a triangle with area . The perimeter of hexagon can be expressed as , where , and are positive integers and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Because the given hexagon is equiangular, each of its interior angles measures , so each angle adjacent to one of these measures . This forces the three angles in every triangle in the figure shown below to be .
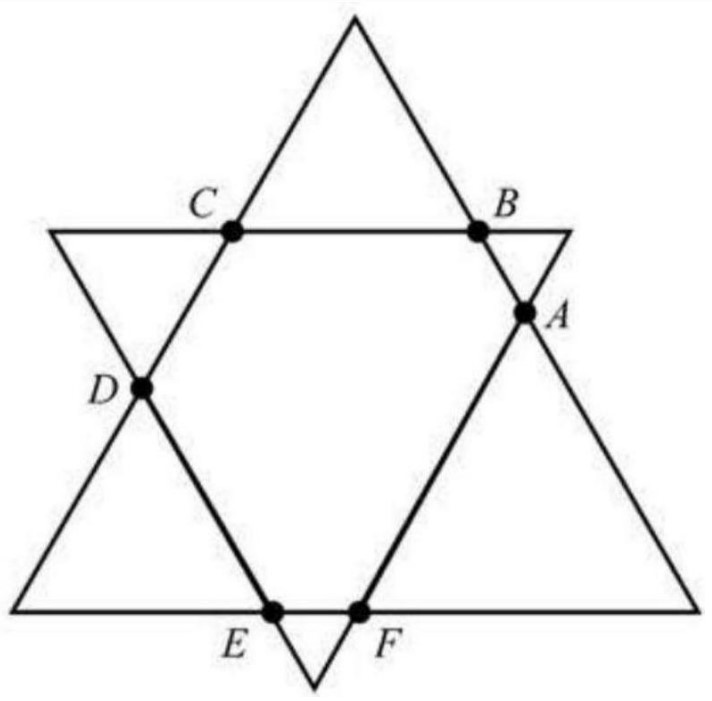
Let and . Then the perimeter of the hexagon is . The triangle determined by lines , and has perimeter , and the triangle determined by lines , and has perimeter . Then
Thus
Adding these equations gives . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions