Problem:
Let △ABC be a scalene triangle. Point P lies on BC so that AP bisects ∠BAC. The line through B perpendicular to AP intersects the line through A parallel to BC at point D. Suppose BP=2 and PC=3. What is AD?
Answer Choices:
A. 8
B. 9
C. 10
D. 11
E. 12
Solution:
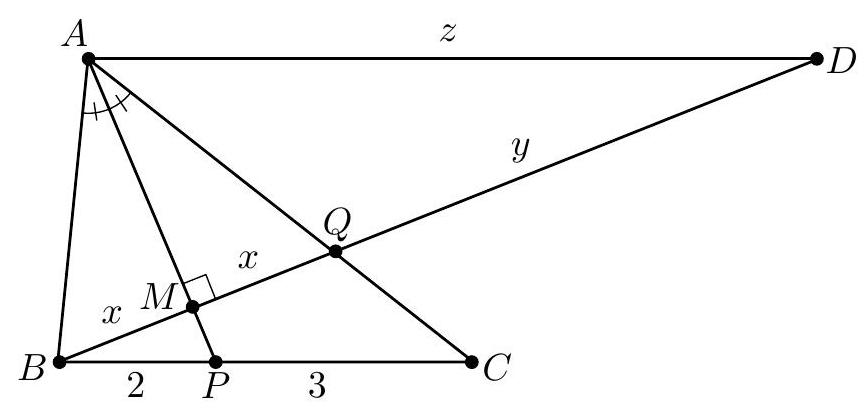
Let Q be the intersection point of AC and BD, as shown.
Because BQ⊥AP and ∠BAP=∠QAP, it follows that △ABQ is isosceles with AB=AQ. Then by the Angle Bisector Theorem,
23=PBPC=ABAC=AQAC=1+AQCQ=1+ADBC=1+AD5.
Solving this equation yields AD=10.
OR
Let M be the intersection point of AP and BQ. As above, △ABQ is isosceles with AB=AQ, so BM=MQ. Let BM=MQ=x,QD=y, and AD=z. Because △AMD and △PMB are similar, it follows that
2z=xx+y=1+xy.
Further, △AQD and △CQB are also similar, so 5z=2xy. It follows that
2z−1=xy=52z
which yields z=(C)10.
The problems on this page are the property of the MAA's American Mathematics Competitions