Problem:
Let ABCD be a rhombus with ∠ADC=46∘. Let E be the midpoint of CD, and let F be the point on BE such that AF is perpendicular to BE. What is the degree measure of ∠BFC?
Answer Choices:
A. 110
B. 111
C. 112
D. 113
E. 114
Solution:
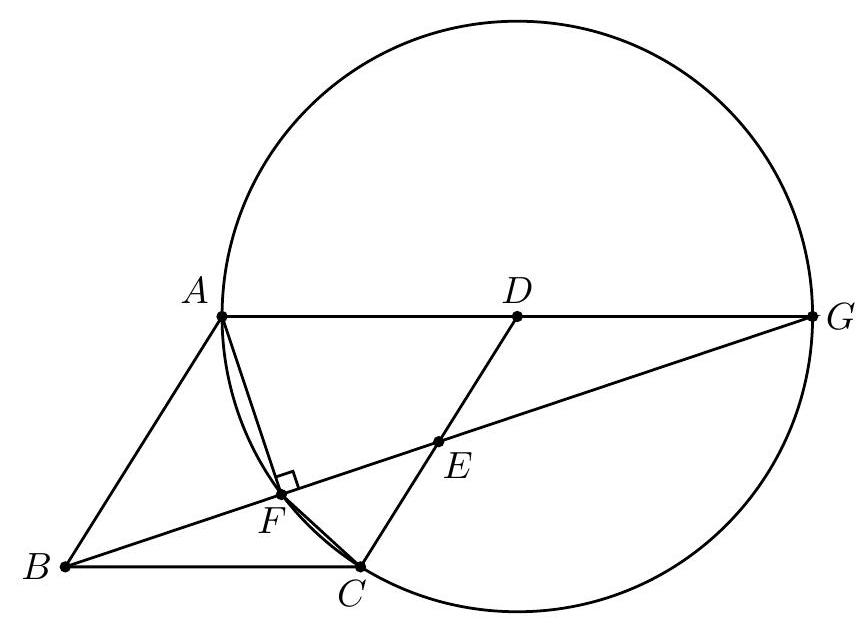
Let G be the intersection point of lines AD and BE. Then △BCE and △GDE are congruent. Points A,C, and G lie on a circle with center at D because AD=GD=CD. Because AF is perpendicular to GF and AG is a diameter of the circle, it follows that point F lies on the circle. Thus
∠GFC=21∠GDC=21(180∘−46∘)=67∘
Therefore ∠BFC=180∘−∠GFC=(D)113∘.
The problems on this page are the property of the MAA's American Mathematics Competitions