¶ 2023 AMC 10B Problem 19
Problem:
Sonya the frog chooses a point uniformly at random lying within the square in the coordinate plane and hops to that point. She then chooses a distance uniformly at random in the interval and a direction uniformly at random from . All her choices are independent. She now hops the chosen distance in the chosen direction. What is the probability that she lands outside the square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
In the figure below, Sonya can hop out of the square only if she occupies a region labeled or after the first hop.
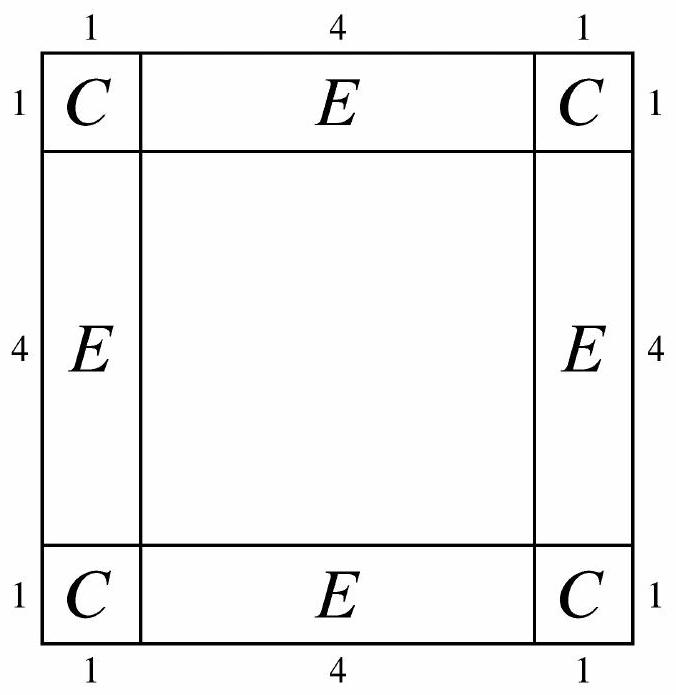
Let be the randomly chosen starting point in the square, and let be the distance of the second hop, where . Suppose , without loss of generality, say in the -region at the top, so . Then Sonya will exit the square if and only if the chosen direction is north and . Because is uniformly distributed in [0,1] and is uniformly distributed in [5,6], the probability that is . The probability that the initial hop lands in any region labeled is , and the probability that the chosen direction is serendipitous is , for a total probability in this case of
The contribution from the corner regions labeled is similar, but two of the four possible directions will lead to Sonya leaving the square this time:
The required probability is
Note: For an square, the probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions