¶ 2023 AMC 10B Problem 20
Problem:
Four congruent semicircles are drawn on the surface of a sphere with radius , as shown, creating a closed curve that divides its surface into two congruent regions. The length of the curve is . What is ?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
The four endpoints of the semicircles determine a square, as shown in the picture.
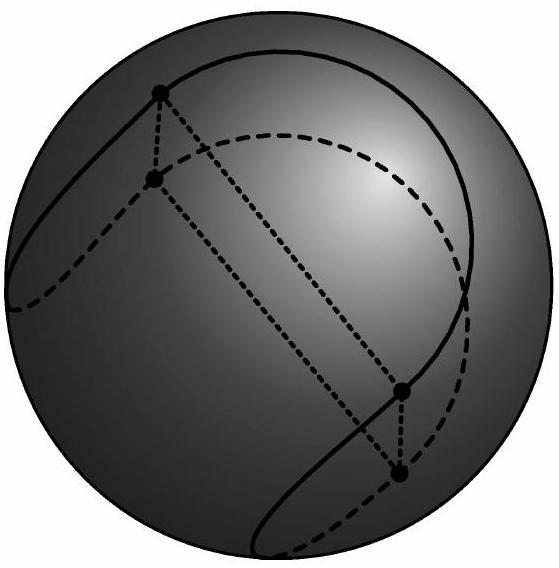
The diagonals of the square are diameters of the sphere, as shown in the next picture.
.jpg)
Each side of the square is a diameter of a semicircle, four of which comprise the closed curve. The diameter of the sphere is 4 , so the diameter of the semicircles (the side length of the square) is . Each semicircle has arc length , so the length of the curve is , and .
The problems on this page are the property of the MAA's American Mathematics Competitions