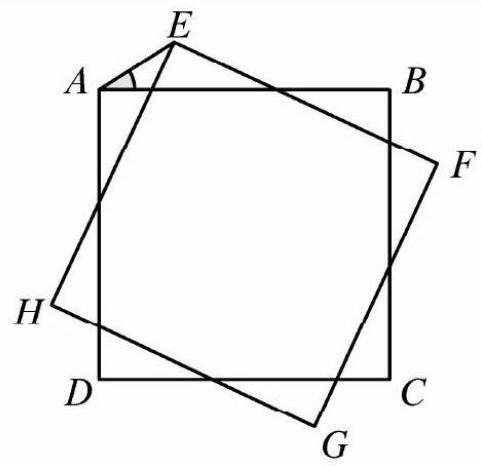
Problem:
Square ABCD is rotated 20∘ clockwise about its center to obtain square EFGH, as shown below. What is the degree measure of ∠EAB?
Answer Choices:
A. 24∘
B. 35∘
C. 30∘
D. 32∘
E. 20∘
Solution:
Let O be the common center of both squares. Because AO=EO, triangle △AOE is isosceles with ∠AOE=20∘. This means ∠EAO=21(180∘−20∘)=80∘. Combined with ∠BAO=45∘, this yields
∠EAB=∠EAO−∠BAO=80∘−45∘=(B)35∘
OR
The vertices ABCDEFG divide the circumscribing circle into 8 arcs. Four are size 20∘, so the other four are 4360∘−4⋅20∘=70∘. Angle ∠EAB is half the measure of the central angle ∠EOB, where O is the center of the circumscribing circle, so ∠EAB=270∘=(B)35∘.
The problems on this page are the property of the MAA's American Mathematics Competitions