¶ 2024 AMC 10A Problem 14
Problem:
One side of an equilateral triangle of height 24 lies on line . A circle of radius 12 is tangent to and is externally tangent to the triangle. The area of the region exterior to the triangle and the circle and bounded by the triangle, the circle, and line can be written as , where , and are positive integers and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The given situation is shown in the figure below, where is the center of the circle, is the point of tangency between the circle and the triangle, is the intersection of line with line , and is the projection of onto .
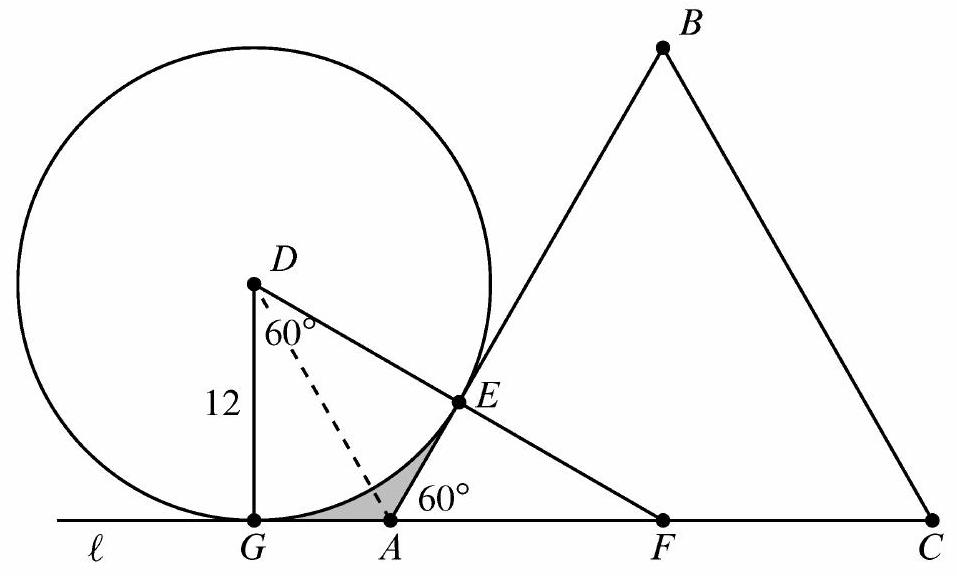
Because and , both and are right triangles. Therefore , and . The area of kite is twice the area of , so it is . The area of the -sector of the circle is . Thus the required area, shaded in the figure, is , and the requested sum is .
The required area is of the difference between the area of a circle of radius 12 and a circumscribed regular hexagon. The hexagon is the union of 6 equilateral triangles of side length . The area of the hexagon is , which equals . The area of the circle is . Then of the difference is , and the requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions