¶ 2025 AMC 10A Problem 10
Problem:
A semicircle has diameter and chord of length parallel to . A smaller semicircle with diameter on and tangent to is cut from the larger semicircle, as shown below.
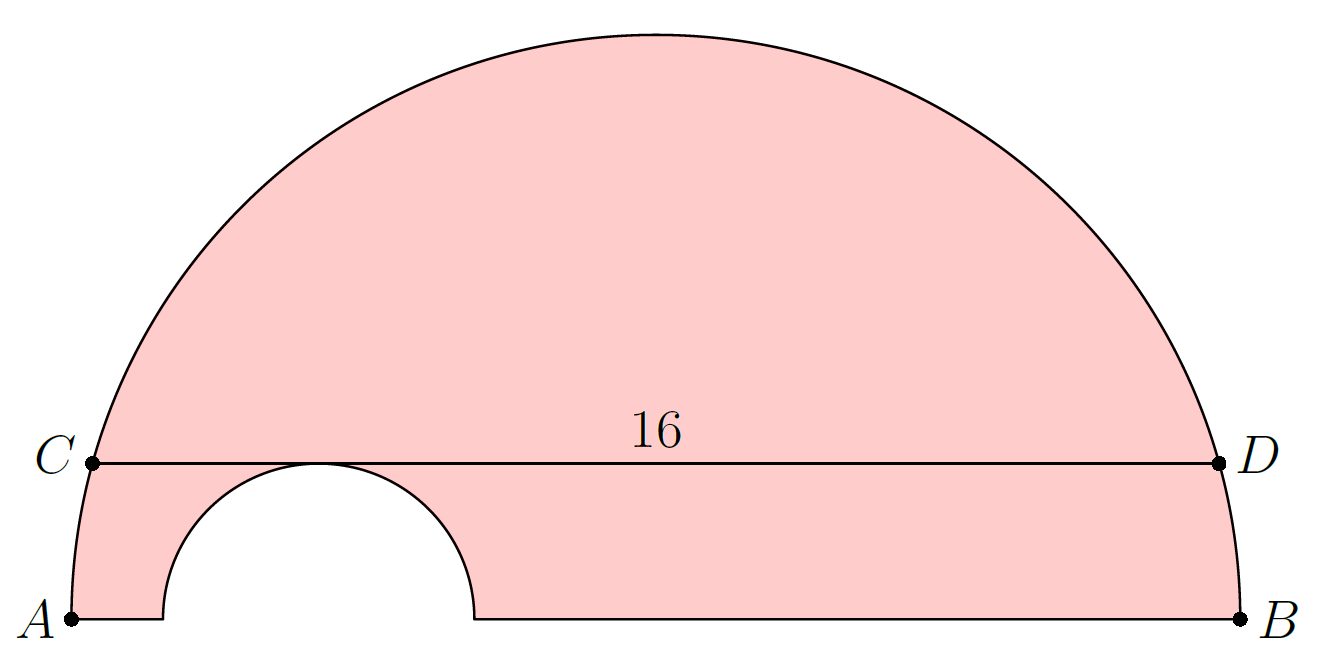
What is the area of the resulting figure, shown shaded?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
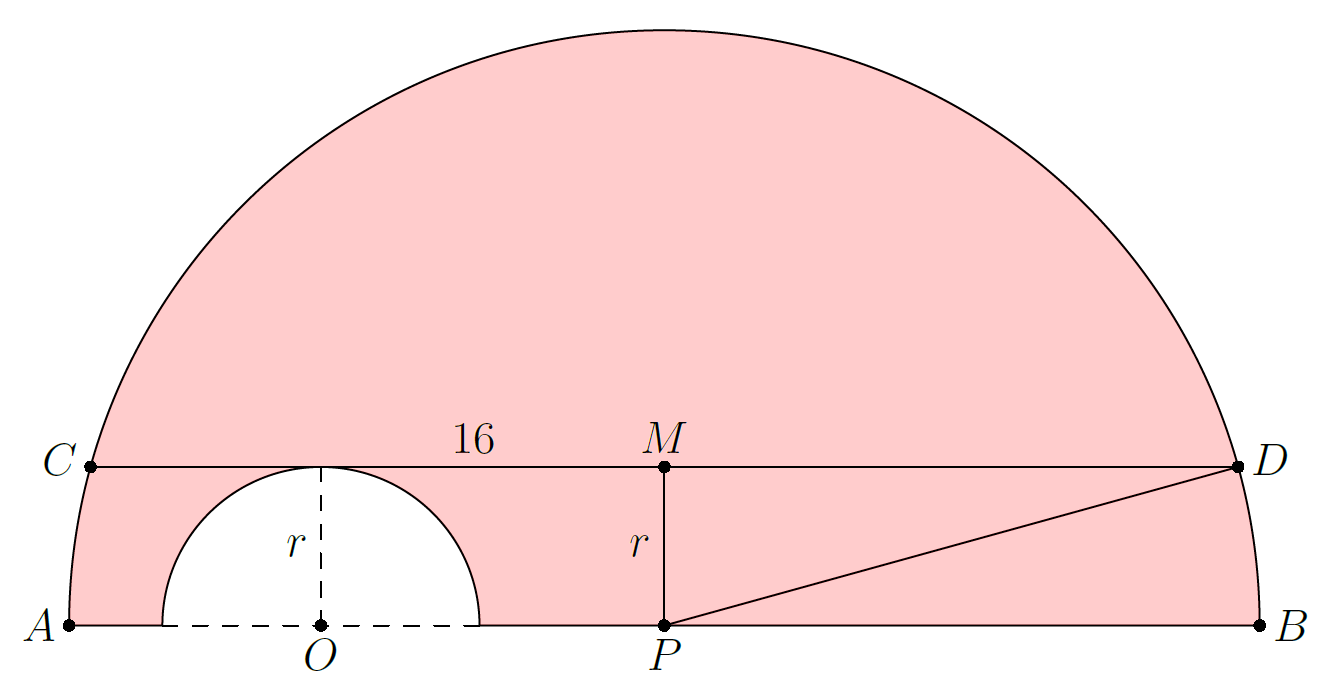
Let the radius of the small circle with center be , as shown in the diagram. Let be the center of the larger (pink) semicircle with radius . Let be the midpoint of the chord . Since is the midpoint of , we have
From the figure,
Applying the Pythagorean Theorem in ,
The required shaded area (the large semicircle minus the small semicircle) is
which gives us the answer
The problems on this page are the property of the MAA's American Mathematics Competitions