Problem:
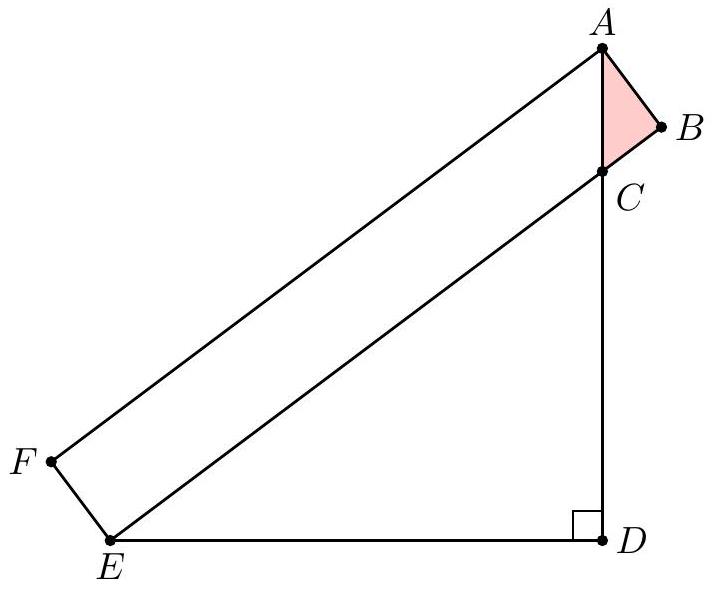
In the figure below, ABEF is a rectangle, AD⊥DE, AF=7, AB=1, and AD=5.
What is the area of △ABC?
Answer Choices:
A. 83
B. 94
C. 8113
D. 157
E. 8115
Solution:
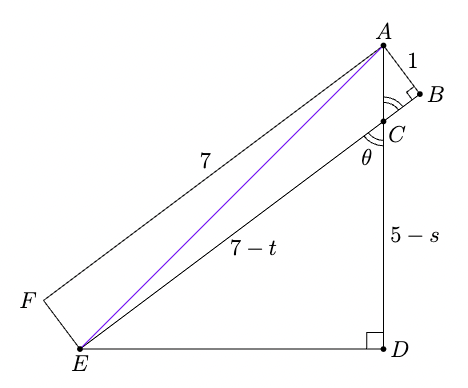
Let the sides and points be as shown in the diagram. By the Pythagorean Theorem applied to the right triangles in the figure,
DE2=AE2−AD2=AB2+AF2−AD2=50−25.25.
so DE=5. Also, from the right triangle,
1+t2=s2(Pythagorean Theorem).
Using similar triangles (△ABC∼△EDC),
DEAB=CEAC⇒51=7−ts⇒5s=7−t.
Substituting s2=1+t2,
25s2=49+t2−14t.
Simplifying,
25t2−t2+25−49+14t=0⇒24t2+14t−24=0⇒12t2+7t−12=0.
Factoring,
12t2+16t−9t−12=0⇒(4t−3)(3t+4)=0.
Hence,
t=43.
The area of △ABC is
[ABC]=21(base)(height)=21⋅1⋅t=21t=(A) 83
Alternate Solution:
From the figure in Solution 1, the triangles △ABC and △EDC are similar. Hence,
△ABC∼△EDC.
By the Pythagorean Theorem, applied to the right triangle,
S2=1+t2(1)
From the similarity of triangles,
7−t5−S=St(2)
Cross-multiplying,
7t−t2=5S−S2(3)
From (1) and (3),
7t+1=5S.
Squaring both sides,
49t2+1+14t=25+25t2.
Simplifying,
24t2+14t−24=0⇒12t2+7t−12=0.
Solving for t,
t=2×12−7+49+576=24−7+25=2418=43.
Therefore, the area of △ABC is
[ABC]=21×(base)×(height)=21×1×t=21t=(A) 83
The problems on this page are the property of the MAA's American Mathematics Competitions