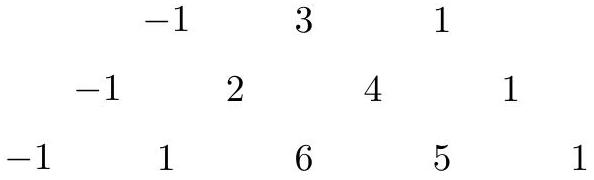Problem:
An array of numbers is constructed beginning with the numbers −1 3 1 in the top row. Each adjacent pair of numbers is summed to produce a number in the next row. Each row begins and ends with −1 and 1, respectively.
If the process continues, one of the rows will sum to 12,288. In that row, what is the third number from the left?
Answer Choices:
A. −29
B. −21
C. −14
D. −8
E. −3
Solution:
We start by defining the notations.
Let the first (top) row be
a1,0=−1,a1,1=3,a1,2=1.
Here, the first subscript denotes the row number, and the second denotes the position within that row (counting from the left, starting at 0).
We now describe how the next rows are formed.
Each subsequent row is obtained by summing adjacent pairs of numbers from the previous row and placing −1 at the beginning and 1 at the end, respectively. Thus
an+1,0an+1,kan+1,last=−1,=an,k−1+an,k(1≤k<last index),=1.
For instance,
Row 1:Row 2:Row 3:−1−1−1321146151.
We next express the general term.
Since the pattern follows Pascal-type addition, each entry in row n can be written as a linear combination of the first-row numbers using binomial coefficients:
an,k=j=0∑2a1,j(k−jn−1).
We determine which row sums to 12,288.
Let Sn denote the sum of all the numbers in row n.
Because the end terms −1 and 1 cancel, each new row doubles the sum of the previous one:
Sn+1=2Sn.
The first row has
S1=−1+3+1=3,
so
Sn=3⋅2n−1.
Setting Sn=12,288 gives
3⋅2n−12n−1n=12,288,=4096=212,=13.
Hence, the desired row is the 13th row.
We finally find the third number from the left.
The third number corresponds to k=2:
a13,2=(−1)(212)+3(112)+1(012)=−66+36+1=(A) -29.
The problems on this page are the property of the MAA's American Mathematics Competitions