Problem:
A circle of radius r is surrounded by three circles, whose radii are 1,2, and 3, all externally tangent to the inner circle and to each other, as shown.
What is r?
Answer Choices:
A. 41
B. 236
C. 113
D. 175
E. 103
Solution:
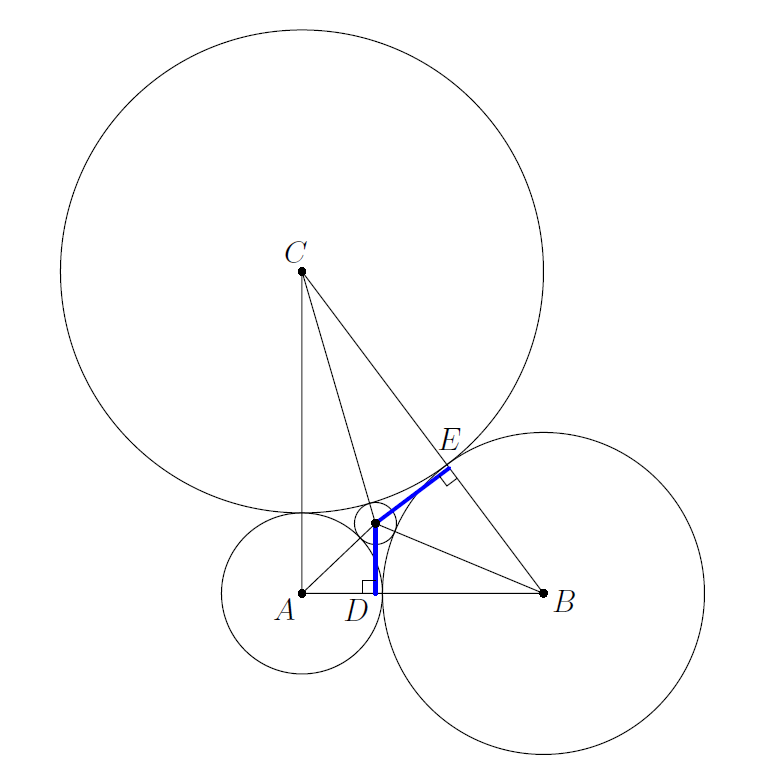
Let the centers of the circles with radii r,1,2, and 3 be O,A,B, and C respectively.
Since
AB=1+2=3,AC=1+3=4,BC=2+3=5,
the triangle ABC is a right-angled triangle with the right angle at B. Place coordinates so that
A(0,0),B(3,0),C(3,4).
Let D be the foot of the perpendicular from O to AB, and E be the foot from O to BC.
Set
OD=y,OE=x,
so that O has coordinates (3−x,y). Since each circle is tangent externally to its neighbors,
OA=r+1,OB=r+2,OC=r+3.
Therefore, using the Pythagorean Theorem:
OA2OB2OC2=x2+y2=(r+1)2=(3−x)2+y2=(r+2)2=x2+(y−4)2=(r+3)2(1)(2)(3)
Subtract (2) from (1) and (3) to eliminate y2 and x2 respectively:
(1)−(2): (3−x)2−x2=(r+2)2−(r+1)2⟹9−6x=2r+3⟹x=1−3r.
(3)−(2): (y−4)2−y2=(r+3)2−(r+1)2⟹−8y+16=4r+8⟹y=1−2r.
Now substitute x,y into equation (2):
x2+y2=(r+1)2,
(1−3r)2+(1−2r)2=(r+1)2.
Simplifying gives
23r2+132r−36=0⟹r=(B) 236.
Remark. This is a special case of Descartes’ Kissing Theorem, which states that if 4 circles of curvature k1,k2,k3,k4 are mutually tangent to each other, then
(k1+k2+k3+k4)2=2(k12+k22+k32+k42)
The problems on this page are the property of the MAA's American Mathematics Competitions