Problem:
In an equilateral triangle each interior angle is trisected by a pair of rays. The intersection of the interiors of the middle 20β-angle at each vertex is the interior of a convex hexagon. What is the degree measure of the smallest angle of this hexagon?
Answer Choices:
A. 80
B. 90
C. 100
D. 110
E. 120
Solution:
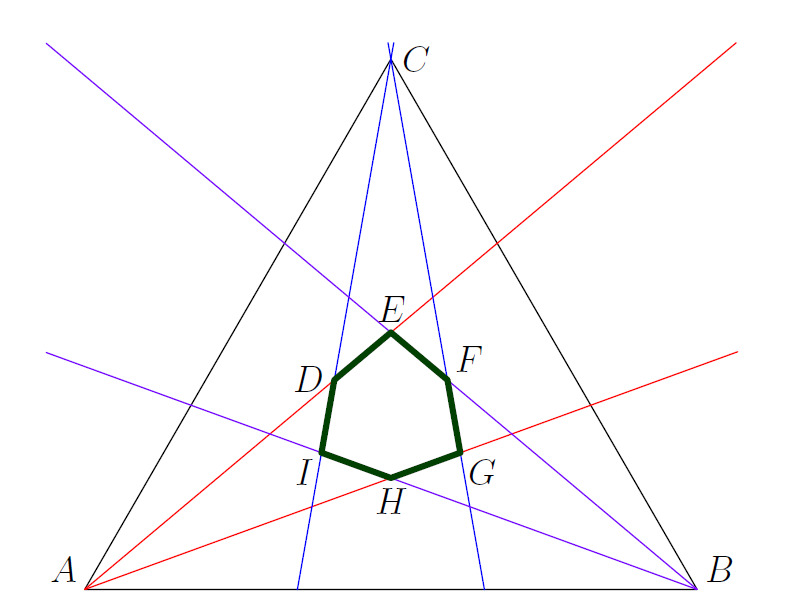
Let ABC be an equilateral triangle with side AB horizontal. Each interior angle is 60β and is trisected into three 20β angles.
At A let the trisectors (starting from AB and going toward AC) be the rays β1β,β2β; at B the trisectors (from BA toward BC) be m1β,m2β; at C (from CA toward CB) be n1β,n2β.
The middle 20β-angle at each vertex is the region between β1β,β2β, between m1β,m2β, and between n1β,n2β respectively.
Measure directions from the positive x-axis (along AB):
-
AB has direction 0β, and AC has direction 60β. Hence β1β,β2β have directions
β (β1β)=20β,β (β2β)=40β.
-
At B, the sides BA,BC have directions 180β and 120β, so the trisectors are
β (m2β)=160β,β (m1β)=140β.
-
At C, the sides CA,CB have directions 240β and 300β, so
β (n1β)=260β,β (n2β)=280β.
The hexagon is the intersection of the three middle 20β sectors; its sides lie on the six lines β1β,β2β,m1β,m2β,n1β,n2β. One checks from the picture that its vertices are the intersections
(β1β,m2β), (β1β,n2β), (β2β,m1β), (β2β,n1β), (m1β,n1β), (m2β,n2β).
The angle between two lines with directions Ξ±,Ξ² is min{β£Ξ±βΞ²β£,360βββ£Ξ±βΞ²β£}.
Thus for these pairs we get
(β1β,m2β):(β1β,n2β):(β2β,m1β):(β2β,n1β):(m1β,n1β):(m2β,n2β):ββ£20ββ160ββ£=140β, 360βββ£20ββ280ββ£=100β,β£40ββ140ββ£=100β, 360βββ£40ββ260ββ£=140β,β£140ββ260ββ£=100β,β£160ββ280ββ£=120β (exterior), so interior =140β.β
Hence the interior angles of the hexagon are three 100β angles and three 140β angles. Therefore the smallest angle of the hexagon is
(C) 100β
The problems on this page are the property of the MAA's American Mathematics Competitions
