¶ 2025 AMC 10B Problem 12
¶ Problem:
The figure below shows an equilateral triangle, a rhombus with a angle, and a regular hexagon, each of them containing some mutually tangent congruent disks. Let and respectively, denote the ratio in each case of the total area of the disks to the area of the enclosing polygon. Which of the following is true?
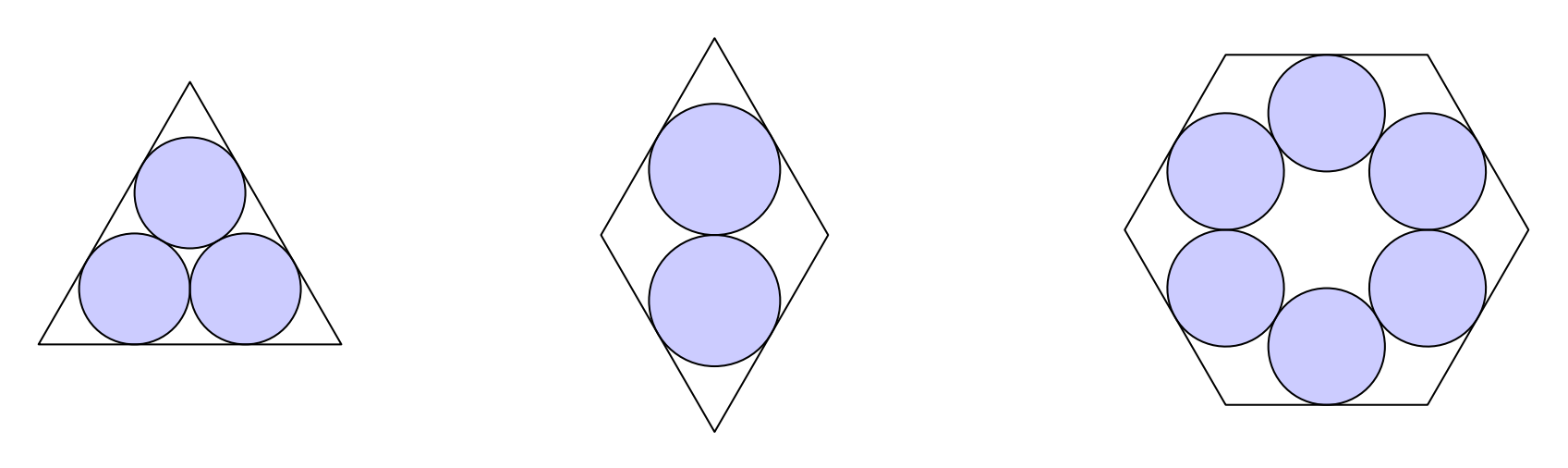
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
Let be the inradius of an equilateral triangle of side length and its area . We'll first deal with the equilateral triangle.
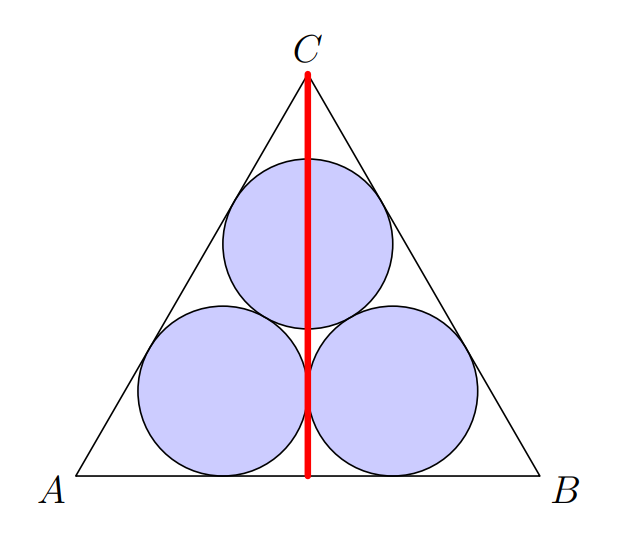
Note that if we draw the perpendicular, each blue circle is simply an incircle of the right triangle. Suppose the side length of the equilateral triangle is , so
(this comes from the fact in a right triangle with legs and hypotenuse , the inradius is ). For what will become apparent later, we note
Now, let's move onto the rhombus and hexagon:
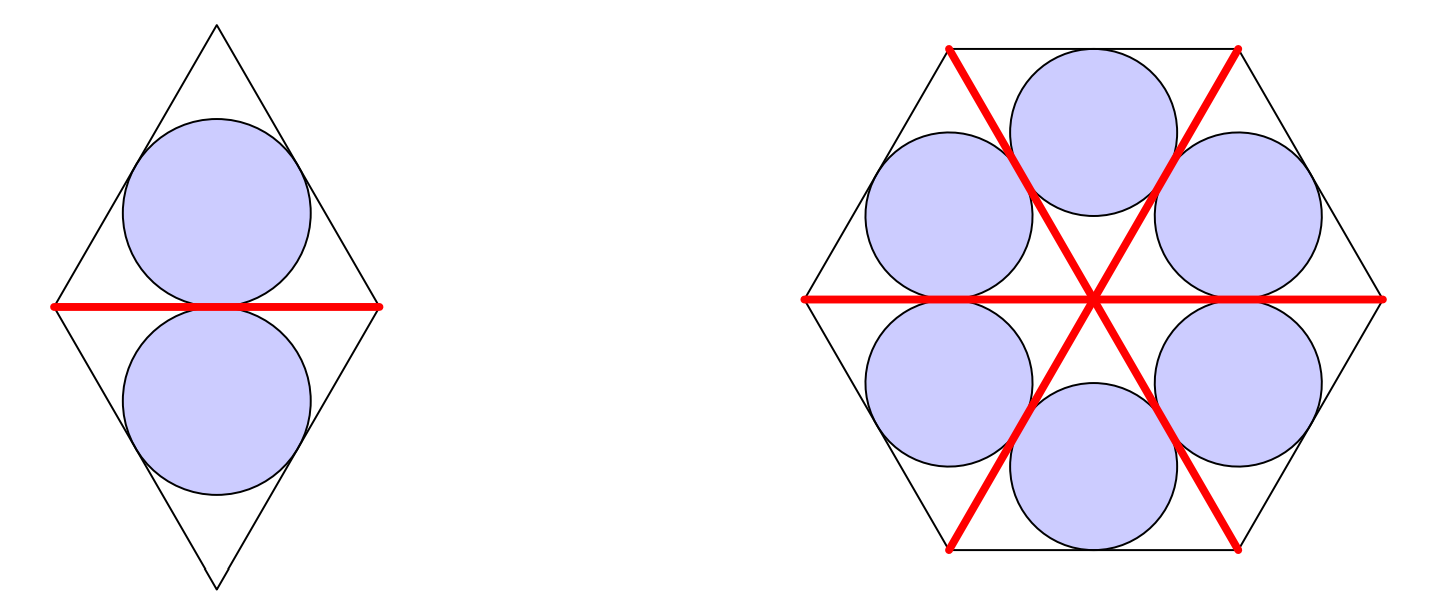
In this case, each circle can be described as an incircle of an equilateral triangle. More specifically, suppose the side length of both figures is . Then, the equilateral triangles in both figures have side lengths , so the radii of all blue circles above is .
We can therefore conclude that
so .
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions