¶ 2025 AMC 10B Problem 16
¶ Problem:
A circle has been divided into sectors of different sizes. Then of the sectors are painted red, painted green, and painted blue so that no two neighboring sectors are painted the same color. One such coloring is shown below. How many different colorings are possible?
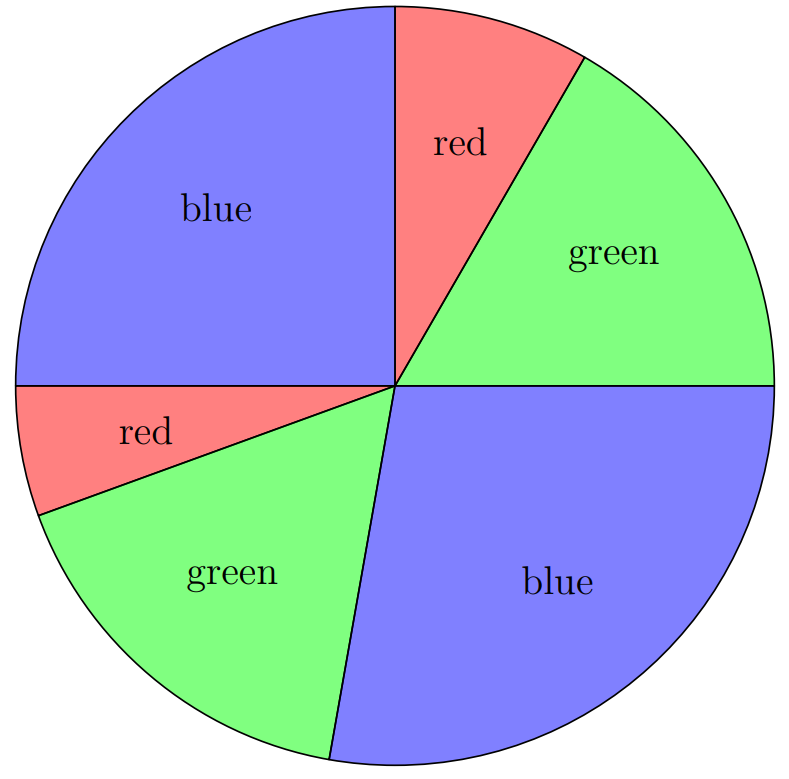
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
There are two cases on how the colors can be distributed:
Case 1: Every color is diametrically opposite itself.
For example if the sectors numbered in clockwise order are , one color would be , another would be , and another would be . There are ways to assign the colors as such.
Case 2: Only color is diametrically opposite itself.
There are choices for the color and choices for the sector pair for it to cover. Without loss suppose a color covered sectors and . Then we see the two remaining colors must cover sectors and . There are ways to pick which color covers which sector for options in this case.
It is impossible to have exactly or diametrically opposite colors, so the answer is .
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions