¶ 2025 AMC 10B Problem 20
¶ Problem:
Four congruent semicircles are inscribed in a square of side length so that their diameters are on the sides of the square, one endpoint of each diameter is at a vertex of the square, and adjacent semicircles are tangent to each other. A small circle centered at the center of the square is tangent to each of the four semicircles, as shown below.
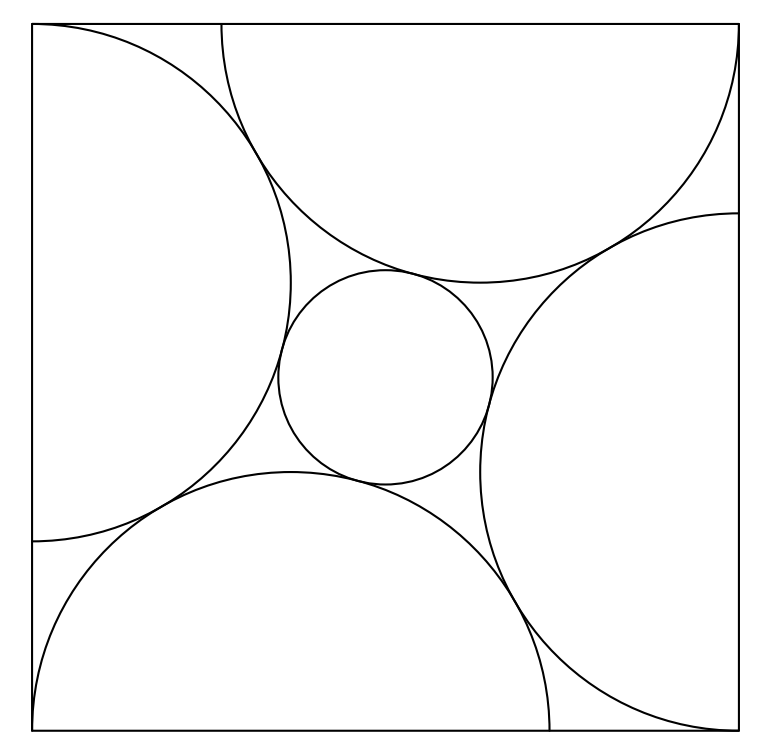
The diameter of the small circle can be written as , where and are integers. What is
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
Let the square be , and the semicircles centered at , as shown below. Let be the radius of the semicircles.
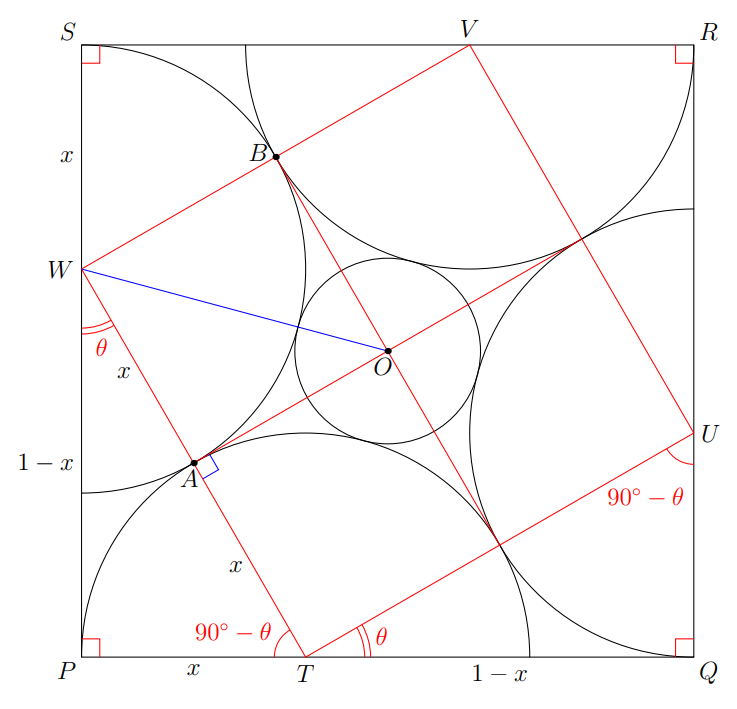
Note that as the semicircles are tangent, (as are radii and are collinear). Thus, is a triangle, and . Thus, we have
Now suppose the small circle has center . Note that (as is a square centered at by symmetry). As the inner circle is tangent to each semicircle,
If we let the radius of the small circle be , we get
so the diameter is , which gives . Thus,
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions