¶ 2025 AMC 10B Problem 25
¶ Problem:
Square has sides of length . Points and lie on and , respectively, with and . A path begins along the segment from to and continues by reflecting against the sides of (with congruent incoming and outgoing angles). If the path hits a vertex of the square, it terminates there; otherwise it continues forever. At which vertex does the path terminate?
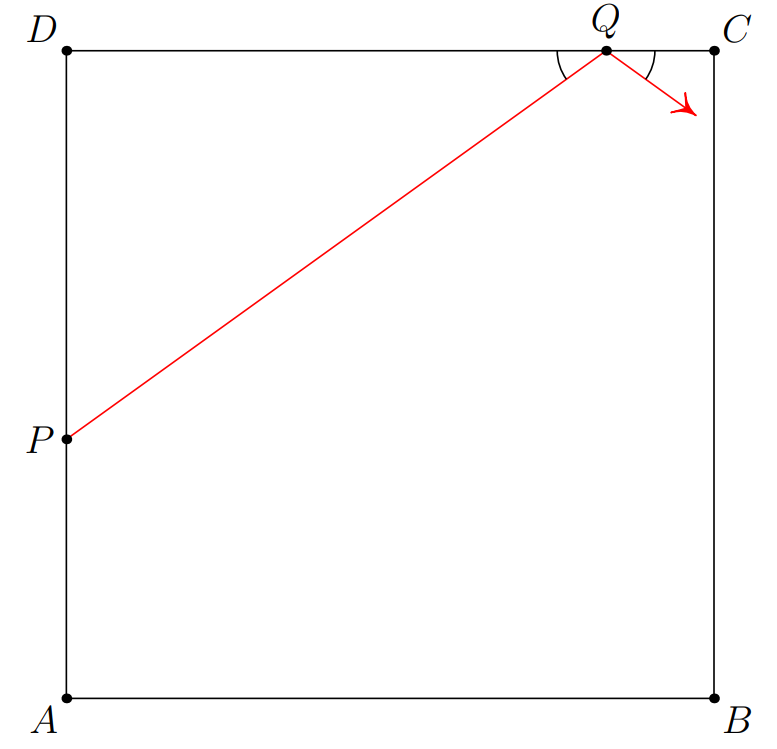
Answer Choices:
A.
B.
C.
D.
E. The path continues forever
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
The square has a side length and is placed in the coordinate plane as
When the path reflects off the sides of the square at equal angles, we can unfold the motion:
- Reflect the square repeatedly across its sides, tiling the plane with congruent squares.
- In this unfolded tiling, the trajectory is a straight line passing through and .
The path hits a vertex of the original square precisely when the line passes through the lattice points . We will first find the equation of the line through . Point lies on with . Since and ,
Point lies on with . Since and ,
Thus, the line through and is
Since we want the points to pass through and , let's assume and .
From , we have:
From the above, it is clear that:
Substituting into , we get:
So we have reduced the problem to solving the simpler Diophantine equation .
Now, we solve for the smallest values of and from . The smallest positive value of ,which works when gives us . At this point, we can draw a quick diagram shown below and find that the vertex is .
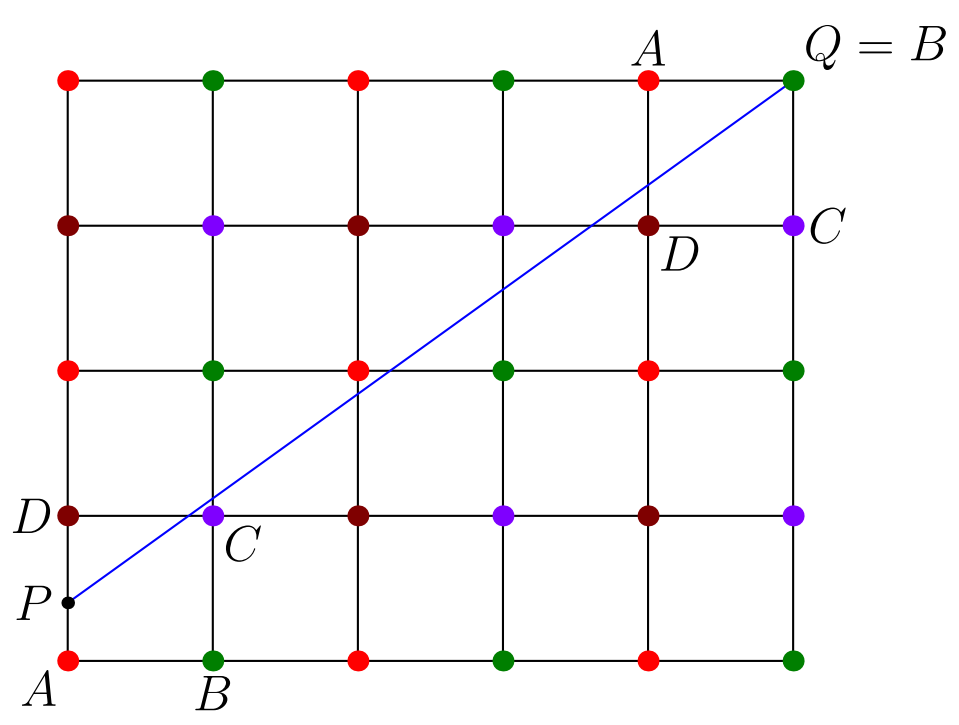
Figure 1: The above diagram shows the unfolded
Remark. If you haven't seen this concept before, this might be something new. Let's work through an example of unfolding these manually.
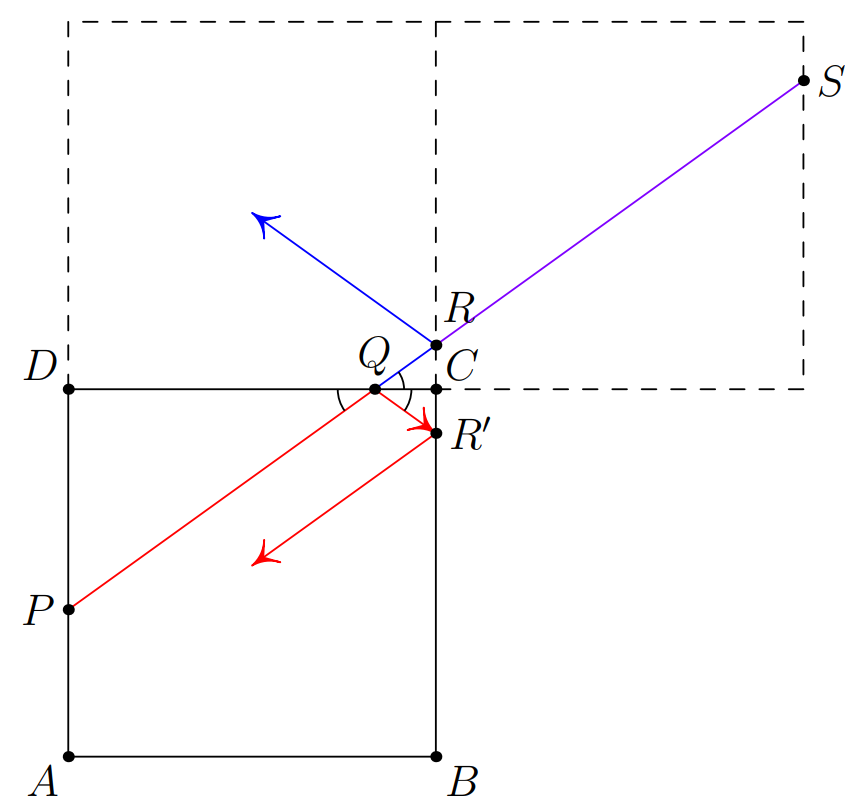
We can take a look at the diagram above, and the first few reflections. As the beam reflects at , it becomes very hard to track it. However, what if we pretended that the wall never existed, and that the beam could keep going?
At that point we reach the point , where as our beam (red) reached the point . Note that and are reflections in , as . This means that to find (and the path of the beam), we can instead follow the straight beam into the blue area, find , and then reflect it to find .
We can keep going. As the straight beam with no walls enters the purple segment, we see that the blue ray is a reflection of the purple segment by the same logic. But since the blue arrow from is a reflection of the red arrow from , we are simply chasing reflections.
By continuously chasing reflections in this manner we obtain our original image above, and can then find the pattern between vertices to find where it hits a vertex.
Remark. We can extract the answer more rigorously, as follows: each pair describes how many squares we move by reflection, both horizontally and vertically. The parity of determines which vertex of the original square is reached:
For our first hit,
so the corresponding vertex in the original square is .
Remark. We can also find generic solutions to the above Diophantine equation using the method below:
From ,
Work modulo :
Therefore, we can Write as
Plug into we obtain:
Therefore
Recall
We are moving forward along the ray from through , so we want the smallest nonnegative giving a positive . Taking ,
Thus, the first vertex of the tiling hit by the line is
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions