¶ 2025 AMC 10B Problem 5
¶ Problem:
In , , , and . Let be the center of the circle containing points . What is the degree measure of
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
Let be the circumcenter of . Since , we can say that is obtuse and hence contained within one half of the circle as shown.
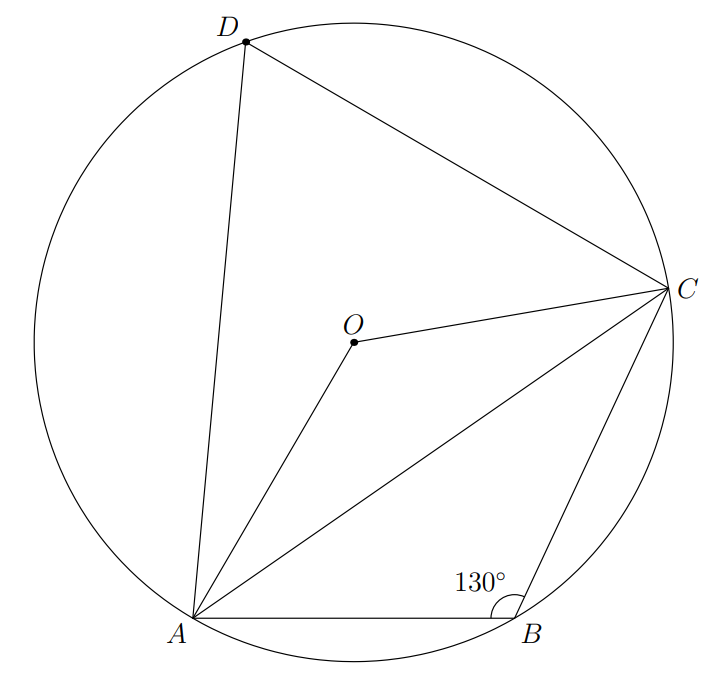
Let be a point on the opposite side of the arc . Now we have a cyclic quadrilateral . As opposite angles in a cyclic quadrilateral add to , we have . Therefore, as central angles are twice the inscribed angles, we have
Finally, we see that the is isosceles and therefore
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions