¶ 2025 AMC 10B Problem 7
¶ Problem:
Frances stands meters directly south of a locked gate in a fence that runs east-west. Immediately behind the fence is a box of chocolates, located meters east of the locked gate. An unlocked gate lies meters east of the box, and another unlocked gate lies meters west of the locked gate. Frances can reach the box by walking toward an unlocked gate, passing through it, and walking toward the box. It happens that the total distance Frances would travel is the same via either unlocked gate. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
💬 Join the Discussion
Stuck on this problem or want to share your approach?
Continue the conversation and see what others are thinking: View Forum Thread
¶ Solution:
Place the locked gate at the origin: . The fence lies along . Frances is at , the box of chocolates at , the east gate at , and the west gate at .
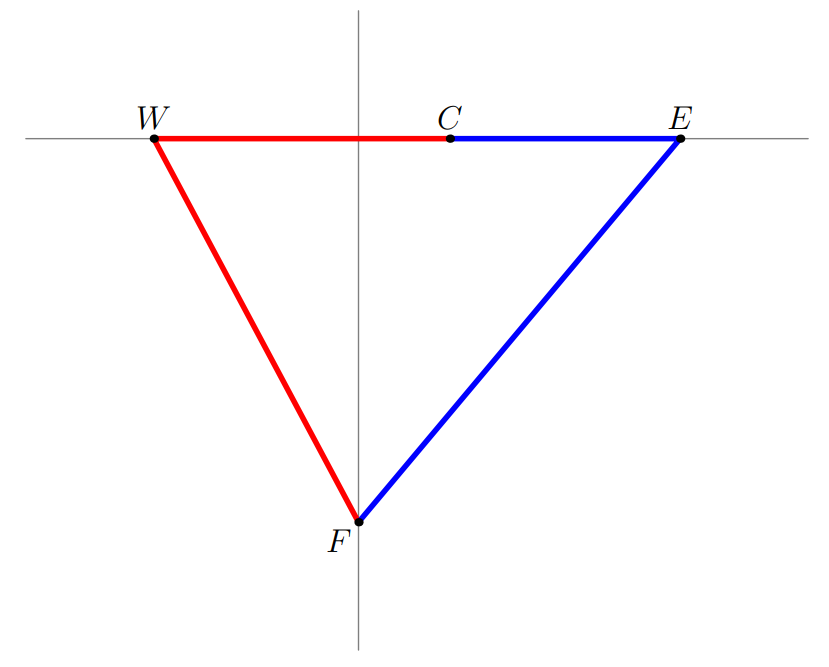
The west gate path (in red) is composed of and , which we can compute as
which gives a total distance of .
The west gate path (in red) is composed of and , which we can compute as
which gives a total distance of .
Since the distances are equal, we equate them to get
Squaring gives
upon which we can expand to get , or
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions